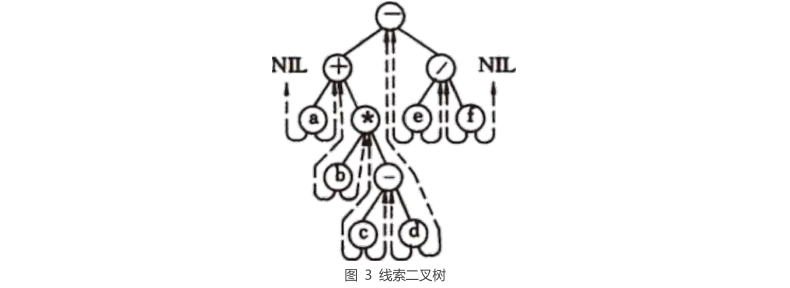
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
| #include <stdio.h>
#include <stdlib.h>
#define TElemType char//宏定义,结点中数据域的类型
//枚举,Link 为 0,Thread 为 1
typedef enum {
Link,
Thread
} PointerTag;
//结点结构构造
typedef struct BiThrNode {
TElemType data;//数据域
struct BiThrNode* lchild,*rchild;//左孩子,右孩子指针域
PointerTag Ltag,Rtag;//标志域,枚举类型
} BiThrNode,*BiThrTree;
BiThrTree pre=NULL;
//采用前序初始化二叉树
//中序和后序只需改变赋值语句的位置即可
void CreateTree(BiThrTree * tree) {
char data;
scanf("%c",&data);
if (data!='#') {
if (!((*tree)=(BiThrNode*)malloc(sizeof(BiThrNode)))) {
printf("申请结点空间失败");
return;
} else {
(*tree)->data=data;//采用前序遍历方式初始化二叉树
CreateTree(&((*tree)->lchild));//初始化左子树
CreateTree(&((*tree)->rchild));//初始化右子树
}
} else {
*tree=NULL;
}
}
//中序对二叉树进行线索化
void InThreading(BiThrTree p) {
//如果当前结点存在
if (p) {
InThreading(p->lchild);//递归当前结点的左子树,进行线索化
//如果当前结点没有左孩子,左标志位设为 1,左指针域指向上一结点 pre
if (!p->lchild) {
p->Ltag=Thread;
p->lchild=pre;
}
//如果 pre 没有右孩子,右标志位设为 1,右指针域指向当前结点。
if (pre&&!pre->rchild) {
pre->Rtag=Thread;
pre->rchild=p;
}
pre=p;//pre 指向当前结点
InThreading(p->rchild);//递归右子树进行线索化
}
}
//中序遍历线索二叉树
void InOrderThraverse_Thr(BiThrTree p) {
while(p) {
//一直找左孩子,最后一个为中序序列中排第一的
while(p->Ltag == Link) {
p = p->lchild;
}
printf("%c ", p->data); //操作结点数据
//当结点右标志位为 1 时,直接找到其后继结点
while(p->Rtag == Thread && p->rchild !=NULL) {
p = p->rchild;
printf("%c ", p->data);
}
//否则,按照中序遍历的规律,找其右子树中最左下的结点,也就是继续循环遍历
p = p->rchild;
}
}
int main() {
BiThrTree t;
printf("输入前序二叉树:\n");
CreateTree(&t);
InThreading(t);
printf("输出中序序列:\n");
InOrderThraverse_Thr(t);
return 0;
}
|