一 概述
1
2
3
| 1.什么是八皇后问题
2.八皇后问题的解决思路
3.示例代码
|
二 什么是八皇后问题
1
2
3
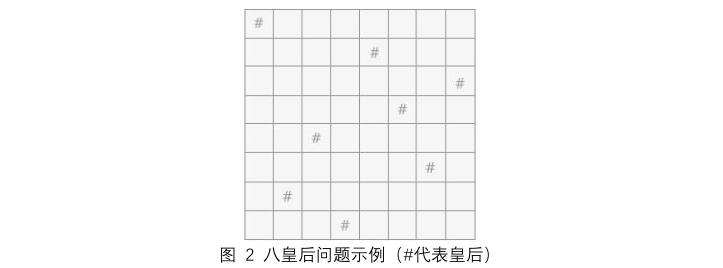
| 八皇后问题是以国际象棋为背景的问题:
有八个皇后(可以当成八个棋子),如何在 8*8 的棋盘中放置八个皇后,
使得任意两个皇后都不在同一条横线、纵线或者斜线上。
|
三 八皇后问题的解决思路
1
2
3
4
5
6
7
8
| 八皇后问题是使用回溯算法解决的典型案例。算法的解决思路是:
1.从棋盘的第一行开始,从第一个位置开始,依次判断当前位置是否能够放置皇后,
判断的依据为:同该行之前的所有行中皇后的所在位置进行比较,
如果在同一列,或者在同一条斜线上(斜线有两条,为正方形的两个对角线),都不符合要求,继续检验后序的位置。
2.如果该行所有位置都不符合要求,则回溯到前一行,改变皇后的位置,继续试探。
3.如果试探到最后一行,所有皇后摆放完毕,则直接打印出 8*8 的棋盘。
最后一定要记得将棋盘恢复原样,避免影响下一次摆放。
|
四 示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include <stdio.h>
int Queenes[8] = { 0 }, Counts = 0;
int Check(int line, int list) {
int index;
//遍历该行之前的所有行
for (index = 0; index < line; index++) {
//挨个取出前面行中皇后所在位置的列坐标
int data = Queenes[index];
//如果在同一列,该位置不能放
if (list == data) {
return 0;
}
//如果当前位置的斜上方有皇后,在一条斜线上,也不行
if ((index + data) == (line + list)) {
return 0;
}
//如果当前位置的斜下方有皇后,在一条斜线上,也不行
if ((index - data) == (line - list)) {
return 0;
}
}
//如果以上情况都不是,当前位置就可以放皇后
return 1;
}
//输出语句
void print()
{
int line;
for (line = 0; line < 8; line++)
{
int list;
for (list = 0; list < Queenes[line]; list++) {
printf("0");
}
printf("#");
for (list = Queenes[line] + 1; list < 8; list++) {
printf("0");
}
printf("\n");
}
printf("================\n");
}
void eight_queen(int line) {
//在数组中为0-7列
int list;
for (list = 0; list < 8; list++) {
//对于固定的行列,检查是否和之前的皇后位置冲突
if (Check(line, list)) {
//不冲突,以行为下标的数组位置记录列数
Queenes[line] = list;
//如果最后一样也不冲突,证明为一个正确的摆法
if (line == 7) {
//统计摆法的Counts加1
Counts++;
//输出这个摆法
print();
//每次成功,都要将数组重归为0
Queenes[line] = 0;
return;
}
//继续判断下一样皇后的摆法,递归
eight_queen(line + 1);
//不管成功失败,该位置都要重新归0,以便重复使用。
Queenes[line] = 0;
}
}
}
int main() {
//调用回溯函数,参数0表示从棋盘的第一行开始判断
eight_queen(0);
printf("摆放的方式有%d种", Counts);
system("pause");
return 0;
}
|
大家可以自己运行一下程序,查看运行结果,由于八皇后问题有 92 种摆法,这里不一一列举
五 参考

