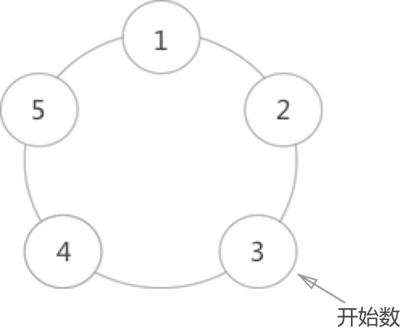
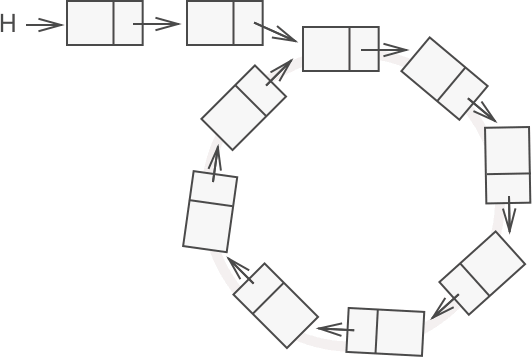
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
| #include <stdio.h>
#include <stdlib.h>
typedef struct node{
int number;
struct node * next;
}person;
person * initLink(int n){
person * head=(person*)malloc(sizeof(person));
head->number=1;
head->next=NULL;
person * cyclic=head;
for (int i=2; i<=n; i++) {
person * body=(person*)malloc(sizeof(person));
body->number=i;
body->next=NULL;
cyclic->next=body;
cyclic=cyclic->next;
}
// 首尾相连
cyclic->next=head;
return head;
}
void findAndKillK(person * head,int k,int m){
person * tail=head;
// 找到链表第一个结点的上一个结点, 为删除操作做准备
while (tail->next!=head) {
tail=tail->next;
}
person * p=head;
// 找到编号为 k 的人
while (p->number!=k) {
tail=p;
p=p->next;
}
// 从编号为 k 的人开始, 只有符合 p->next==p 时, 说明链表中除了 p 结点, 所有编号都出列了
while (p->next!=p) {
// 找到从 p 报数 1 开始, 报 m 的人, 并且还要知道数 m-1 的人的位置 tail,方便
// 做删除操作
for (int i=1; i<m; i++) {
tail=p;
p=p->next;
}
// 从链表上将p结点摘下来
tail->next=p->next;
printf("出列人的编号为:%d\n",p->number);
free(p);
// 继续使用 p 指针指向出列编号的下一个编号, 游戏继续
p=tail->next;
}
printf("出列人的编号为:%d\n",p->number);
free(p);
}
int main() {
printf("输入圆桌上的人数n:");
int n;
scanf("%d",&n);
person * head=initLink(n);
printf("从第k人开始报数(k>1且k<%d):",n);
int k;
scanf("%d",&k);
printf("数到m的人出列:");
int m;
scanf("%d",&m);
findAndKillK(head, k, m);
return 0;
}
/*
输入圆桌上的人数n:5
从第k人开始报数(k>1且k<5):3
数到m的人出列:2
出列人的编号为:4
出列人的编号为:1
出列人的编号为:3
出列人的编号为:2
出列人的编号为:5
*/
|