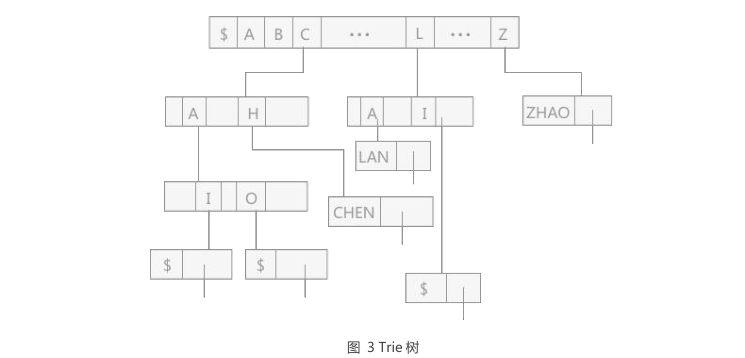
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| typedef enum {LEFT,BRANCH} NodeKind; //定义结点类型
typedef struct {//定义存储关键字的数组
char a[20];
int num;
} KeysType;
//定义结点结构
typedef struct TrieNode {
NodeKind kind;//结点类型
union {
struct {
KeysType k;
struct TrieNode *infoptr;
} lf; //叶子结点
struct {
struct TrieNode *ptr[27];
int num;
} bh; //分支结点
};
}*TrieTree;
//求字符 a 在字母表中的位置
int ord(char a) {
int b = a - 'A'+1;
return b;
}
//查找函数
TrieTree SearchTrie(TrieTree T, KeysType K) {
int i=0;
TrieTree p = T;
while (i < K.num) {
if (p && p->kind==BRANCH && p->bh.ptr[ord(K.a[i])]) {
i++;
p = p->bh.ptr[ord(K.a[i])];
} else {
break;
}
}
if (p) {
return p->lf.infoptr;
}
return p;
}
|