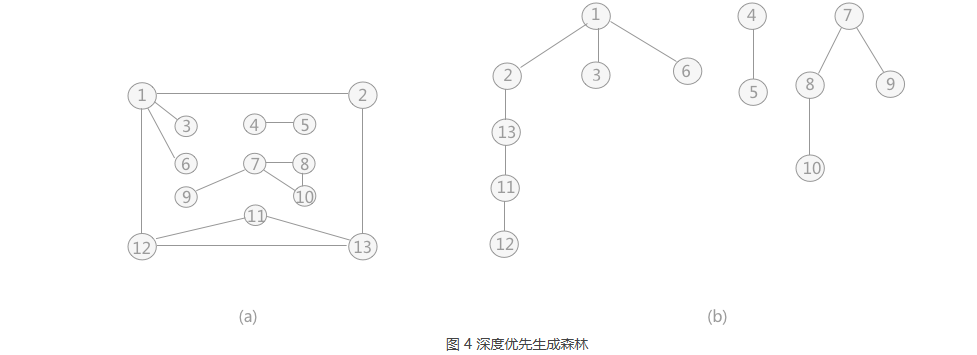
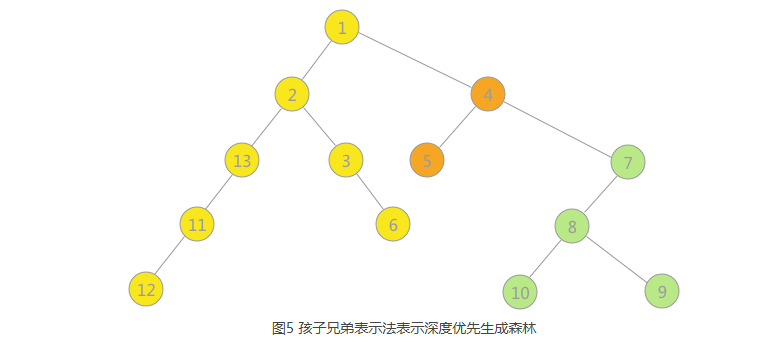
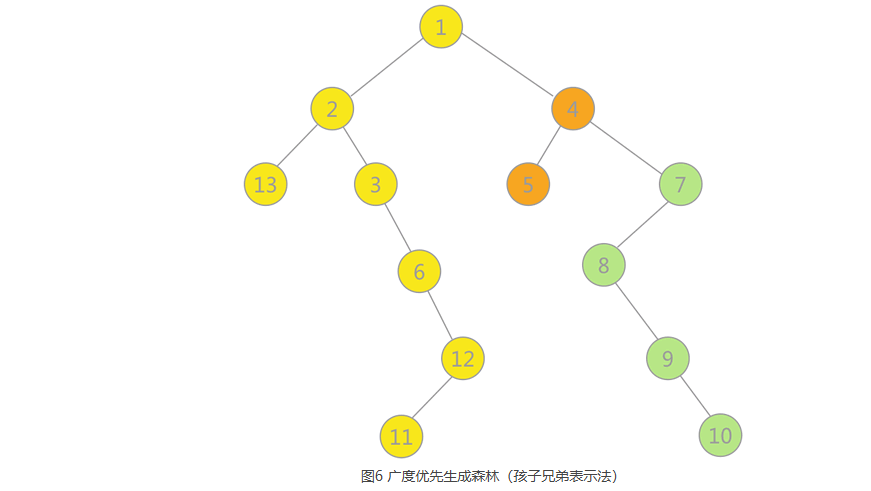
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
| #include <stdio.h>
#include <stdlib.h>
#define MAX_VERtEX_NUM 20 //顶点的最大个数
#define VRType int //表示顶点之间的关系的变量类型
#define InfoType char //存储弧或者边额外信息的指针变量类型
#define VertexType int //图中顶点的数据类型
typedef enum{false,true}bool; //定义bool型常量
bool visited[MAX_VERtEX_NUM]; //设置全局数组,记录标记顶点是否被访问过
typedef struct {
VRType adj; //对于无权图,用 1 或 0 表示是否相邻;对于带权图,直接为权值。
InfoType * info; //弧或边额外含有的信息指针
}ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];
typedef struct {
VertexType vexs[MAX_VERtEX_NUM]; //存储图中顶点数据
AdjMatrix arcs; //二维数组,记录顶点之间的关系
int vexnum,arcnum; //记录图的顶点数和弧(边)数
}MGraph;
typedef struct CSNode{
VertexType data;
struct CSNode * lchild;//孩子结点
struct CSNode * nextsibling;//兄弟结点
}*CSTree,CSNode;
typedef struct Queue{
CSTree data;//队列中存放的为树结点
struct Queue * next;
}Queue;
//根据顶点本身数据,判断出顶点在二维数组中的位置
int LocateVex(MGraph * G,VertexType v){
int i=0;
//遍历一维数组,找到变量v
for (; i<G->vexnum; i++) {
if (G->vexs[i]==v) {
break;
}
}
//如果找不到,输出提示语句,返回-1
if (i>G->vexnum) {
printf("no such vertex.\n");
return -1;
}
return i;
}
//构造无向图
void CreateDN(MGraph *G){
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->vexs[i]));
}
for (int i=0; i<G->vexnum; i++) {
for (int j=0; j<G->vexnum; j++) {
G->arcs[i][j].adj=0;
G->arcs[i][j].info=NULL;
}
}
for (int i=0; i<G->arcnum; i++) {
int v1,v2;
scanf("%d,%d",&v1,&v2);
int n=LocateVex(G, v1);
int m=LocateVex(G, v2);
if (m==-1 ||n==-1) {
printf("no this vertex\n");
return;
}
G->arcs[n][m].adj=1;
G->arcs[m][n].adj=1;//无向图的二阶矩阵沿主对角线对称
}
}
int FirstAdjVex(MGraph G,int v)
{
//查找与数组下标为v的顶点之间有边的顶点,返回它在数组中的下标
for(int i = 0; i<G.vexnum; i++){
if( G.arcs[v][i].adj ){
return i;
}
}
return -1;
}
int NextAdjVex(MGraph G,int v,int w)
{
//从前一个访问位置w的下一个位置开始,查找之间有边的顶点
for(int i = w+1; i<G.vexnum; i++){
if(G.arcs[v][i].adj){
return i;
}
}
return -1;
}
//初始化队列
void InitQueue(Queue ** Q){
(*Q)=(Queue*)malloc(sizeof(Queue));
(*Q)->next=NULL;
}
//结点v进队列
void EnQueue(Queue **Q,CSTree T){
Queue * element=(Queue*)malloc(sizeof(Queue));
element->data=T;
element->next=NULL;
Queue * temp=(*Q);
while (temp->next!=NULL) {
temp=temp->next;
}
temp->next=element;
}
//队头元素出队列
void DeQueue(Queue **Q,CSTree *u){
(*u)=(*Q)->next->data;
(*Q)->next=(*Q)->next->next;
}
//判断队列是否为空
bool QueueEmpty(Queue *Q){
if (Q->next==NULL) {
return true;
}
return false;
}
void BFSTree(MGraph G,int v,CSTree*T){
CSTree q=NULL;
Queue * Q;
InitQueue(&Q);
//根结点入队
EnQueue(&Q, (*T));
//当队列为空时,证明遍历完成
while (!QueueEmpty(Q)) {
bool first=true;
//队列首个结点出队
DeQueue(&Q,&q);
//判断结点中的数据在数组中的具体位置
int v=LocateVex(&G,q->data);
//已经访问过的更改其标志位
visited[v]=true;
//遍历以出队结点为起始点的所有邻接点
for (int w=FirstAdjVex(G,v); w>=0; w=NextAdjVex(G,v, w)) {
//标志位为false,证明未遍历过
if (!visited[w]) {
//新建一个结点 p,存放当前遍历的顶点
CSTree p=(CSTree)malloc(sizeof(CSNode));
p->data=G.vexs[w];
p->lchild=NULL;
p->nextsibling=NULL;
//当前结点入队
EnQueue(&Q, p);
//更改标志位
visited[w]=true;
//如果是出队顶点的第一个邻接点,设置p结点为其左孩子
if (first) {
q->lchild=p;
first=false;
}
//否则设置其为兄弟结点
else{
q->nextsibling=p;
}
q=p;
}
}
}
}
//广度优先搜索生成森林并转化为二叉树
void BFSForest(MGraph G,CSTree *T){
(*T)=NULL;
//每个顶点的标记为初始化为false
for (int v=0; v<G.vexnum; v++) {
visited[v]=false;
}
CSTree q=NULL;
//遍历图中所有的顶点
for (int v=0; v<G.vexnum; v++) {
//如果该顶点的标记位为false,证明未访问过
if (!(visited[v])) {
//新建一个结点,表示该顶点
CSTree p=(CSTree)malloc(sizeof(CSNode));
p->data=G.vexs[v];
p->lchild=NULL;
p->nextsibling=NULL;
//如果树未空,则该顶点作为树的树根
if (!(*T)) {
(*T)=p;
}
//该顶点作为树根的兄弟结点
else{
q->nextsibling=p;
}
//每次都要把q指针指向新的结点,为下次添加结点做铺垫
q=p;
//以该结点为起始点,构建广度优先生成树
BFSTree(G,v,&p);
}
}
}
//前序遍历二叉树
void PreOrderTraverse(CSTree T){
if (T) {
printf("%d ",T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->nextsibling);
}
return;
}
int main() {
MGraph G;//建立一个图的变量
CreateDN(&G);//初始化图
CSTree T;
BFSForest(G, &T);
PreOrderTraverse(T);
return 0;
}
|