数据结构与算法基础——第02周-案例引入(2.2)
一 案例概述
- 案例1——1元多项式的运算:实现两个多项式加、减、乘运算
- 案例2 ——稀疏多项式
- 案例3——图书管理系统
二 一元多项式的运算:实现两个多项式加、减、乘运算
Pn(x)=P0+P1X+P2X2+...+PnXn
线性表P=(P0,P1,P2,...Pn)(每一项的指数i隐含在其系数pi的序号中)
例如:P(x)=10+5x-4x2+3x3+2x4
用数组表示为:
| 指数(下标i) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 系数p[i] | 10 | 5 | -4 | 3 | 2 |
Rn(x)=Pn(x)+Qm(x)用线性表表示为:R=(p0+q0,p1+q1,p2+q2,...pm+qm,pm+1,...pn)
三 稀疏多项式
3.1 什么是稀疏多项式
S(x)=1+3x10000+2x20000
将会造成存储空间,很大的浪费,怎么办?
3.2 多项式非零项的数组表示
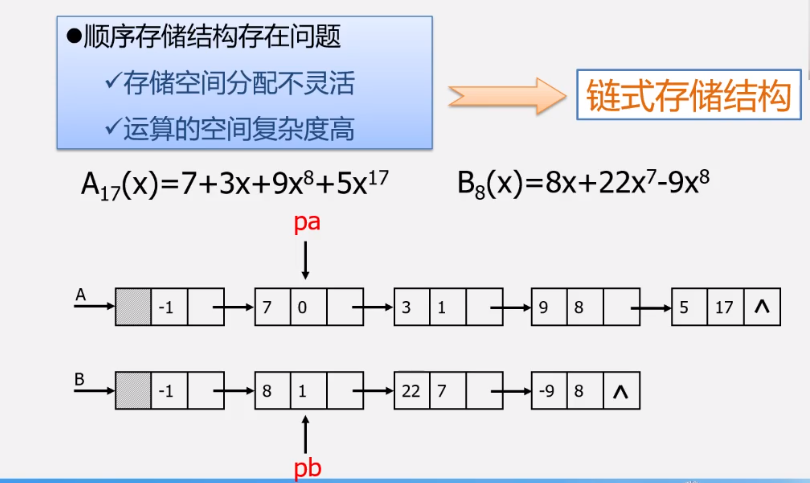
A(x)=7+3x+9x8+5x17
| 下标i | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 系数a[i] | 7 | 3 | 9 | 5 |
| 指数 | 0 | 1 | 8 | 17 |
B(x)=8x+22x7-9x8
| 下标i | 0 | 1 | 2 |
|---|---|---|---|
| 系数a[i] | 8 | 22 | -9 |
| 指数 | 1 | 7 | 8 |
- Pn(x)=p1xe1+p2xe2+...+pmxem可以转换为线性表P=((p1,e1),(p2,e2),...,(pm,em))
- 线性表A=((7,0),(3,1),(9,8),(5,17)),线性表B=((8,1),(22,-7),(-9,8))
3.3 稀疏多项式的运算
1 | 线性表A=((7,0),(3,1),(9,8),(5,17)) |
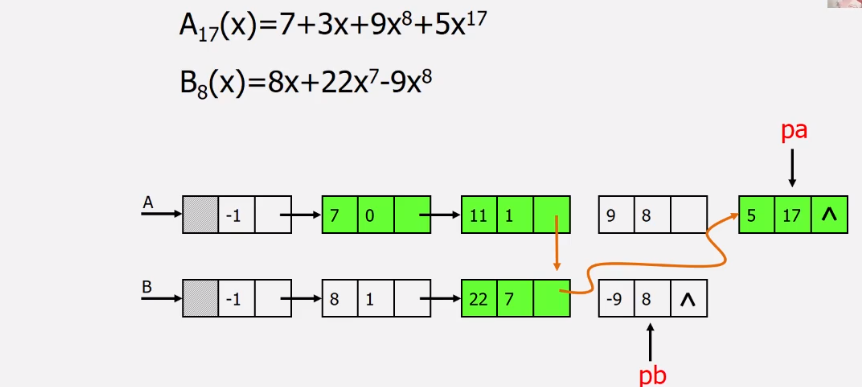
操作过程:
- 创建一个新数组c
- 分别从头遍历比较a和b的每一项
- 指数相同,对应系数相加,若其和不为零,则在c中增加一个新项
- 指数不同,则将指数较小的项复制到c中
- 一个多项式已遍历完毕时,将另一个剩余项依次复制到c中即可(数组c多大何时呢?)
3.4 改变存储结构
3.5 多项式相加
四 图书管理系统
4.1 图书管理系统介绍
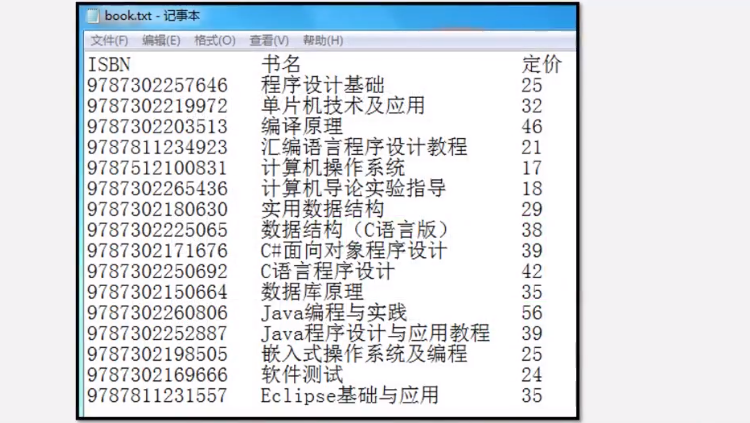
需要进行操作
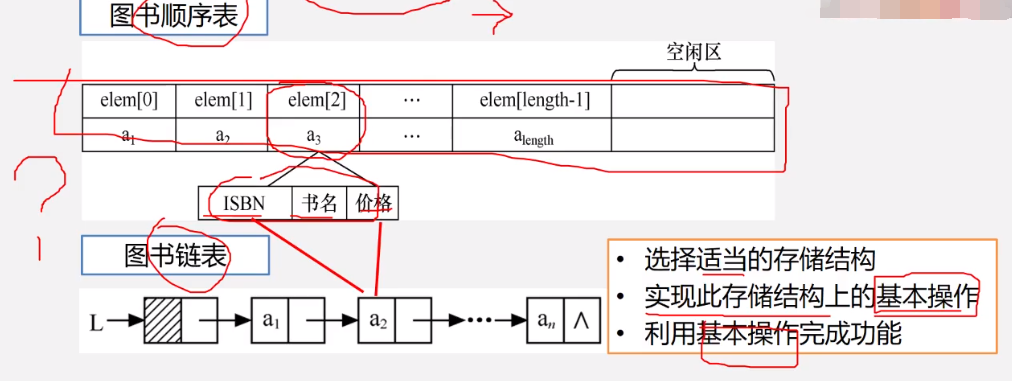
- 查找、插入、删除、修改、排序、计数
- 图书表抽象为线性表
- 表中每本图书抽象线性表中数据元素
4.2 将数组转换为链表
五 总结
- 线性表中数据元素的类型可以为简单类型,也可以为复杂类型
- 许多实际应用问题所涉的基本操作有很大相似性,不应为每个具体应用单独编写一个程序
- 从具体应用抽象出共性的逻辑结构和基本操作(抽象数据类型),然后实现其存储结构和基本操作