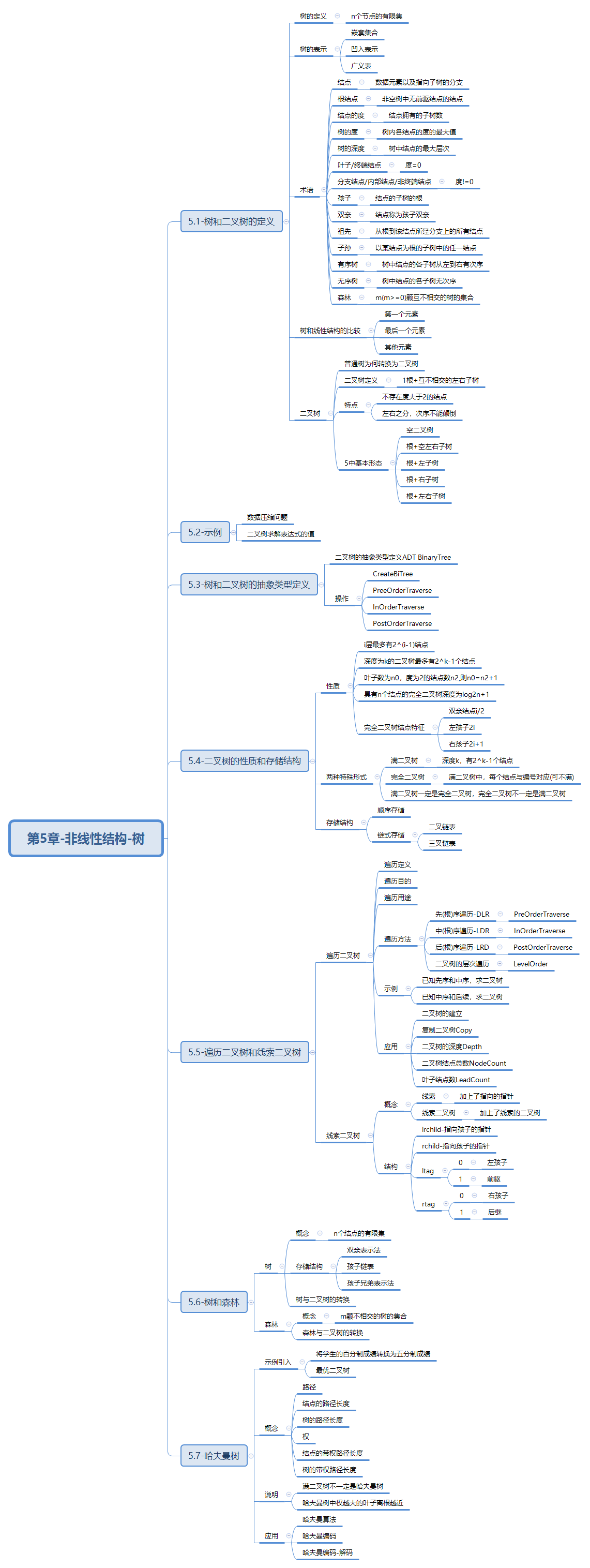
青岛大学数据结构与算法——第5章
一 概述
- 树和二叉树的定义
- 示例
- 树和二叉树的抽象类型定义
- 二叉树的性质和存储结构
- 遍历二叉树和线索二叉树
- 树和森林
- 哈夫曼树
二 树和二叉树的定义
2.1 树的定义
n个节点的有限集
2.2 树的表示
- 嵌套集合
- 凹入表示
- 广义表
2.3 术语
- 结点:数据元素以及指向子树的分支
- 根结点:非空树中无前驱结点的结点
- 结点的度:结点拥有的子树数
- 树的度:树内各结点的度的最大值
- 树的深度:树中结点的最大层次
- 叶子/终端结点:度=0
- 分支结点/内部结点/非终端结点:度!=0
- 孩子:结点的子树的根
- 双亲:结点称为孩子双亲
- 祖先:从根到该结点所经分支上的所有结点
- 子孙:以某结点为根的子树中的任一结点
- 有序树:树中结点的各子树从左到右有次序
- 无序树:树中结点的各子树无次序
- 森林:m(m>=0)颗互不相交的树的集合
2.4 树和线性结构的比较
- 第一个元素
- 最后一个元素
- 其他元素
2.5 二叉树
- 普通树为何转换为二叉树
- 二叉树定义:1根+互不相交的左右子树
- 特点:不存在度大于2的结点、左右之分,次序不能颠倒
- 5中基本形态:空二叉树、根+空左右子树、根+左子树、根+右子树、根+左右子树
三 示例
- 数据压缩问题
- 二叉树求解表达式的值
四 树和二叉树的抽象类型定义
4.1 二叉树的抽象类型定义ADT BinaryTree
4.2 操作
- CreateBiTree
- PreeOrderTraverse
- InOrderTraverse
- PostOrderTraverse
五 二叉树的性质和存储结构
5.1 性质
- i层最多有2^(i-1)结点
- 深度为k的二叉树最多有2^k-1个结点
- 叶子数为n0,度为2的结点数n2,则n0=n2+1
- 具有n个结点的完全二叉树深度为log2n+1
- 完全二叉树结点特征:双亲结点i/2、左孩子2i、右孩子2i+1
5.2 两种特殊形式
- 满二叉树:深度k,有2^k-1个结点
- 完全二叉树:满二叉树中,每个结点与编号对应(可不满)
- 满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
5.3 存储结构
- 顺序存储
- 链式存储:二叉链表、三叉链表
六 遍历二叉树和线索二叉树
6.1 遍历二叉树
- 遍历定义
- 遍历目的
- 遍历用途
- 遍历方法:先(根)序遍历-DLR、中(根)序遍历-LDR、后(根)序遍历-LRD、二叉树的层次遍历
- 示例:已知先序和中序,求二叉树、已知中序和后续,求二叉树
- 应用:二叉树的建立、复制二叉树Copy、二叉树的深度Depth、二叉树结点总数NodeCount、叶子结点数LeadCount
6.2 线索二叉树
- 概念:线索(加上了指向的指针)、线索二叉树(加上了线索的二叉树)
- 结构:lrchild-指向孩子的指针、rchild-指向孩子的指针、ltag、rtag
七 树和森林
7.1 树
- 概念:n个结点的有限集
- 存储结构:双亲表示法、孩子链表、孩子兄弟表示法
- 树与二叉树的转换
7.2 森林
- 概念:m颗不相交的树的集合
- 森林与二叉树的转换
八 哈夫曼树
8.1 示例引入
- 将学生的百分制成绩转换为五分制成绩
- 最优二叉树
8.2 概念
- 路径
- 结点的路径长度
- 树的路径长度
- 权
- 结点的带权路径长度
- 树的带权路径长度
8.3 说明
- 满二叉树不一定是哈夫曼树
- 哈夫曼树中权越大的叶子离根越近
8.4 应用
- 哈夫曼算法
- 哈夫曼编码
- 哈夫曼编码-解码
九 图示