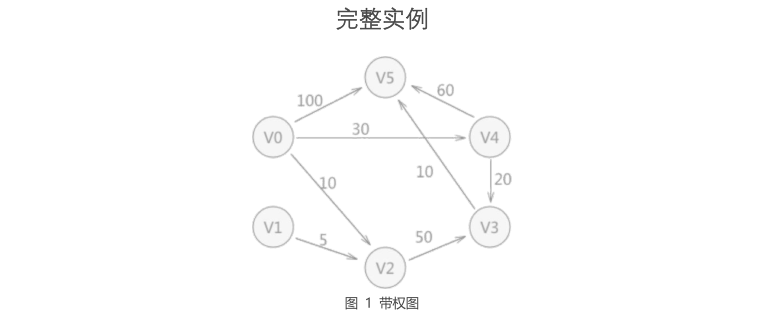
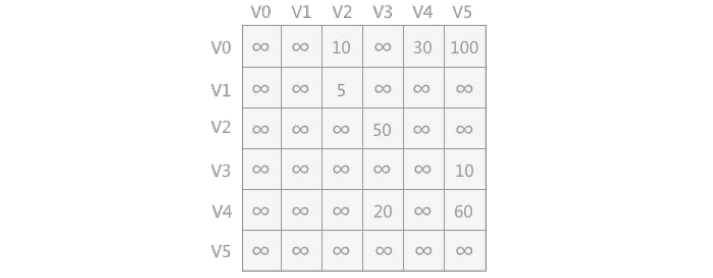
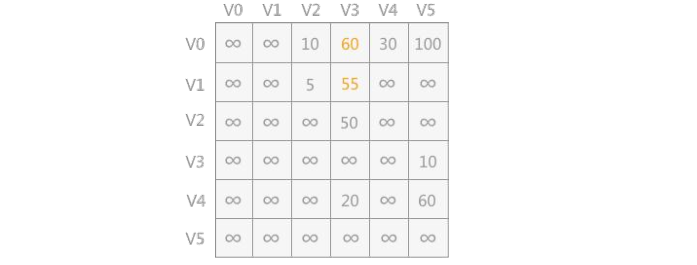
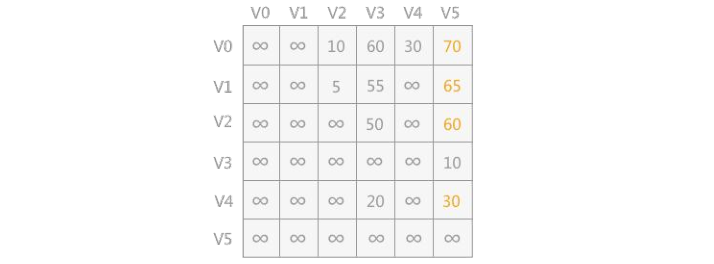
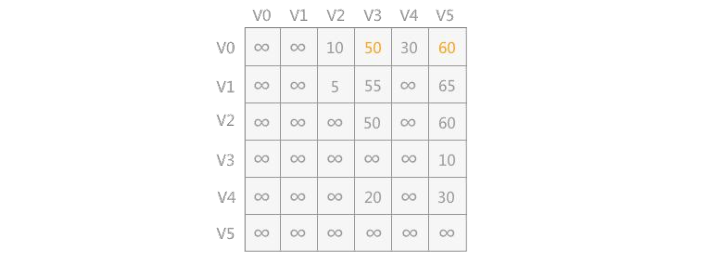
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
| #include <stdio.h>
#define MAX_VERtEX_NUM 20 //顶点的最大个数
#define VRType int //表示弧的权值的类型
#define VertexType int //图中顶点的数据类型
#define INFINITY 65535
typedef struct {
VertexType vexs[MAX_VERtEX_NUM]; //存储图中顶点数据
VRType arcs[MAX_VERtEX_NUM][MAX_VERtEX_NUM]; //二维数组,记录顶点之间的关系
int vexnum,arcnum; //记录图的顶点数和弧(边)数
}MGraph;
typedef int PathMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM]; //用于存储最短路径中经过的顶点的下标
typedef int ShortPathTable[MAX_VERtEX_NUM][MAX_VERtEX_NUM]; //用于存储各个最短路径的权值和
//根据顶点本身数据,判断出顶点在二维数组中的位置
int LocateVex(MGraph * G,VertexType v){
int i=0;
//遍历一维数组,找到变量v
for (; i<G->vexnum; i++) {
if (G->vexs[i]==v) {
break;
}
}
//如果找不到,输出提示语句,返回-1
if (i>G->vexnum) {
printf("no such vertex.\n");
return -1;
}
return i;
}
//构造有向网
void CreateUDG(MGraph *G){
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->vexs[i]));
}
for (int i=0; i<G->vexnum; i++) {
for (int j=0; j<G->vexnum; j++) {
G->arcs[i][j]=INFINITY;
}
}
for (int i=0; i<G->arcnum; i++) {
int v1,v2,w;
scanf("%d,%d,%d",&v1,&v2,&w);
int n=LocateVex(G, v1);
int m=LocateVex(G, v2);
if (m==-1 ||n==-1) {
printf("no this vertex\n");
return;
}
G->arcs[n][m]=w;
}
}
//弗洛伊德算法,其中P二维数组存放各对顶点的最短路径经过的顶点,D二维数组存储各个顶点之间的权值
void ShortestPath_Floyed(MGraph G,PathMatrix *P,ShortPathTable *D){
//对P数组和D数组进行初始化
for (int v=0; v<G.vexnum; v++) {
for (int w=0; w<G.vexnum; w++) {
(*D)[v][w]=G.arcs[v][w];
(*P)[v][w]=-1;
}
}
//拿出每个顶点作为遍历条件
for (int k=0; k<G.vexnum; k++) {
//对于第k个顶点来说,遍历网中任意两个顶点,判断间接的距离是否更短
for (int v=0; v<G.vexnum; v++) {
for (int w=0; w<G.vexnum; w++) {
//判断经过顶点k的距离是否更短,如果判断成立,则存储距离更短的路径
if ((*D)[v][w] > (*D)[v][k] + (*D)[k][w]) {
(*D)[v][w]=(*D)[v][k] + (*D)[k][w];
(*P)[v][w]=k;
}
}
}
}
}
int main(){
MGraph G;
CreateUDG(&G);
PathMatrix P;
ShortPathTable D;
ShortestPath_Floyed(G, &P, &D);
for (int i=0; i<G.vexnum; i++) {
for (int j=0; j<G.vexnum; j++) {
printf("%d ",P[i][j]);
}
printf("\n");
}
for (int i=0; i<G.vexnum; i++) {
for (int j=0; j<G.vexnum; j++) {
printf("%d ",D[i][j]);
}
printf("\n");
}
return 0;
}
|