数据结构与算法基础——第02周-线性表的顺序表示和实现-插入算法(2.4.5)

发表于 分类于 ， ， 阅读时长 ≈ 1 分钟

一 概述

  • 顺序表的插入—演示
  • 顺序表的插入—算法思想
  • 顺序表的插入—代码实现
  • 顺序表的插入—算法分析

二 顺序表的插入—插入不同位置演示

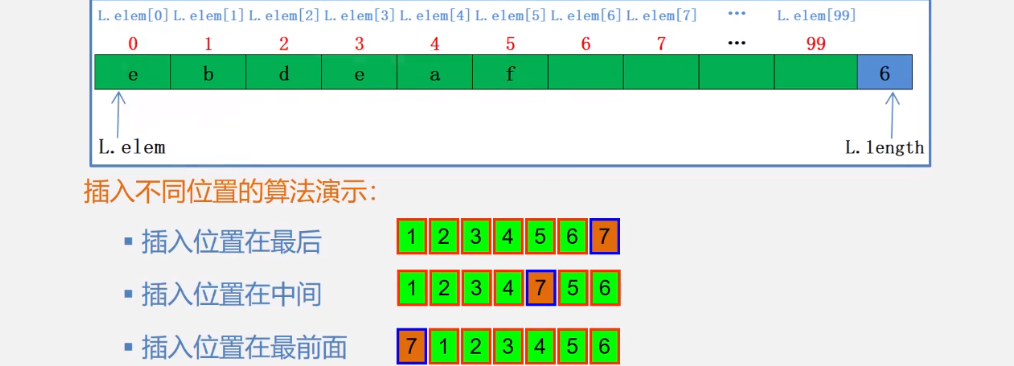
三 顺序表的插入—算法思想

3.1 插入描述

线性表的插入运算是指在表的第i(1<=i<=n+1)个位置上，插入一个新节点e，使长度为n的线性表(a1,...,ai-1,ai,...an)变成长度为n+1的线性表(a1,...ai-1,e,ai,...,an)

3.2 算法思想

  1. 判断插入位置i是否合法
  2. 判断顺序表的存储空间是否已满，若已满返回ERROR。
  3. 将第n至第i位的元素依次向后移动一个位置，空出第i个位置
  4. 将要插入的新元素e放入第i个位置

四 顺序表的插入—代码实现

1
2
3
4
5
6
7
8
9
10
11
Status ListInsert_Sq(SqList &L,int i,ElemType e)
{
 	①if(i<1||i>L.length+1) return ERROR;   //i值不合法
 	②if(L.length==MAXSIZE) return ERROR;   //当前存储空间已满
 	③for(j=L.length-1;j>=i-1;j--)
 		L.elem[j+1]=L.elem[j];            //插入位置及之后的元素后移
    ④L.elem[i-1]=e;                        //将新元素e放入第i个位置
    ⑤L.length++;							  //表长增1
    return OK;
 
}

五 顺序表的插入—算法分析

算法时间主要耗费在移动元素的操作上

  • 若插入在尾结点之后，则根本无需移动(特别快)
  • 若插入在首结点之前，则表中元素全部后移(特别慢)
  • 若要考虑在各种位置插入(共n+1种可能)的平均移动次数，该如何计算？
    Eins=1/(n+1)∑n+1i=1(n-i+1)=1/(n+1)*(n+...+1+0)=1/(n+1)*(n*(n+1)/2)=n/2
  • 顺序表插入算法的平均时间复杂度为O(n)