一 概述
1
2
3
| 1.稀疏矩阵的压缩存储示
2.三元组结构体实现
3.完整代码
|
二 稀疏矩阵的压缩存储示
2.1 概念
1
2
3
4
5
| 本节介绍稀疏矩阵的三元组顺序表压缩存储方式。
通过《矩阵的压缩存储》一节我们知道,稀疏矩阵的压缩存储,至少需要存储以下信息:
1.矩阵中各非 0 元素的值,以及所在矩阵中的行标和列标;
2.矩阵的总行数和总列数;
|
2.2 图示
1
2
3
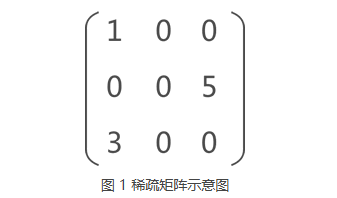
| 例如,图 1 是一个稀疏矩阵,若对其进行压缩存储,矩阵中各非 0 元素的存储状态如图 2 所示:
图 2 的数组中,存储的是三元组(即由 3 部分数据组成的集合),组中数据分别表示(行标,列标,元素值)。
注意,这里矩阵的行标和列标都从 1 开始。
|
| 稀疏矩阵示意图 |
稀疏矩阵的压缩存储示意图 |
 |
 |
三 三元组结构体实现
3.1 三元组代码
C 语言中,三元组需要用结构体实现,如下所示:
1
2
3
4
5
| //三元组结构体
typedef struct {
int i,j;//行标i,列标j
int data;//元素值
}tripl
|
3.2 整个稀疏矩阵代码
1
2
3
4
5
6
7
8
9
10
| 由于稀疏矩阵中非 0 元素有多个,因此需要建立 triple 数组存储各个元素的三元组。
除此之外,考虑到还要存储矩阵的总行数和总列数,因此可以采用以下结构表示整个稀疏矩阵:
可以看到,TSMatrix 是一个结构体,其包含一个三元组数组,以及用于存储矩阵总行数、总列数和非 0 元素个数的变量。
#define number 20
//矩阵的结构表示
typedef struct {
triple data[number];//存储该矩阵中所有非0元素的三元组
int n,m,num;//n和m分别记录矩阵的行数和列数,num记录矩阵中所有的非0元素的个数
}TSMatrix;
|
四 完整代码
假设采用 TSMatrix 结构体存储图 1 中的稀疏矩阵,其 C 语言实现代码应该为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| #include<stdio.h>
#define number 3
typedef struct {
int i,j;
int data;
}triple;
typedef struct {
triple data[number];
int n,m,num;
}TSMatrix;
//输出存储的稀疏矩阵
void display(TSMatrix M);
int main() {
TSMatrix M;
M.m=3;
M.n=3;
M.num=3;
M.data[0].i=1;
M.data[0].j=1;
M.data[0].data=1;
M.data[1].i=2;
M.data[1].j=3;
M.data[1].data=5;
M.data[2].i=3;
M.data[2].j=1;
M.data[2].data=3;
display(M);
return 0;
}
void display(TSMatrix M){
for(int i=1;i<=M.n;i++){
for(int j=1;j<=M.m;j++){
int value =0;
for(int k=0;k<M.num;k++){
if(i == M.data[k].i && j == M.data[k].j){
printf("%d ",M.data[k].data);
value =1;
break;
}
}
if(value == 0)
printf("0 ");
}
printf("\n");
}
}
|
输出结果为:
五 参考
- C语言中文网—三元组顺序表,稀疏矩阵的三元组表示及(C语言)实现

