数据结构与算法——第6章-树-二叉树的顺序存储结构(6.3)

一 概述

1.二叉树的存储形式
2.普通二叉树转完全二叉树
3.完全二叉树的顺序存储

二 二叉树的存储形式

二叉树的存储结构有两种，分别为顺序存储和链式存储。本节先介绍二叉树的顺序存储结构。

二叉树的顺序存储，指的是使用顺序表（数组）存储二叉树。需要注意的是，顺序存储只适用于完全二叉树。
换句话说，只有完全二叉树才可以使用顺序表存储。因此，如果我们想顺序存储普通二叉树，需要提前将普通二叉树转化为完全二叉树。

有读者会说，满二叉树也可以使用顺序存储。要知道，满二叉树也是完全二叉树，因为它满足完全二叉树的所有特征。

三 普通二叉树转完全二叉树

3.1 说明

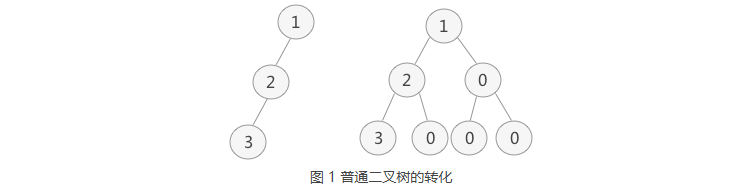
普通二叉树转完全二叉树的方法很简单，只需给二叉树额外添加一些节点，将其"拼凑"成完全二叉树即可。如图 1 所示：
图 1 中，左侧是普通二叉树，右侧是转化后的完全（满）二叉树。

3.2 图示

四 完全二叉树的顺序存储

解决了二叉树的转化问题，接下来学习如何顺序存储完全（满）二叉树。

4.1 完全二叉树图示

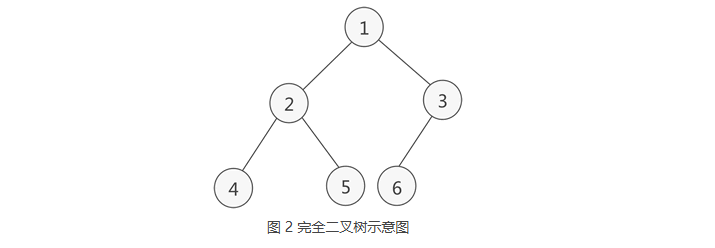
完全二叉树的顺序存储，仅需从根节点开始，按照层次依次将树中节点存储到数组即可。

4.2 完全二叉树存储

一、例如，存储图 2 所示的完全二叉树，其存储状态如图 3 所示：

二、同样，存储由普通二叉树转化来的完全二叉树也是如此。例如，图 1 中普通二叉树的数组存储状态如图 4 所示：

由此，我们就实现了完全二叉树的顺序存储。

五 总结

不仅如此，从顺序表中还原完全二叉树也很简单。
我们知道，完全二叉树具有这样的性质，将树中节点按照层次并从左到右依次标号（1,2,3,...），
若节点 i 有左右孩子，则其左孩子节点为 2*i，右孩子节点为 2*i+1。
此性质可用于还原数组中存储的完全二叉树，也就是实现由图 3 到图 2、由图 4 到图 1 的转变。

编写本节实现代码，需要对二叉树进行层次遍历，这个知识点本章有单独一节做详细介绍，这里不再给出具体的代码实现。

六 参考

• C语言中文网—二叉树的顺序存储结构