数据结构与算法——第9章-查找表-红黑树算法和应用(9.8.1)

发表于 2023-05-13 分类于开发， N-数据与算法，数据结构与算法阅读时长 ≈ 1 分钟

一概述

1.红黑树
2.红黑树特性
3.红黑树图示
4.红黑树高度
5.时间复杂度
6.红黑树调整

二红黑树

红黑树（R-B TREE，全称：Red-Black Tree），本身是一棵二叉查找树，在其基础上附加了两个要求：
1. 树中的每个结点增加了一个用于存储颜色的标志域；
2. 树中没有一条路径比其他任何路径长出两倍，整棵树要接近于“平衡”的状态。

这里所指的路径，指的是从任何一个结点开始，一直到其子孙的叶子结点的长度；
接近于平衡：红黑树并不是平衡二叉树，只是由于对各路径的长度之差有限制，所以近似于平衡的状态。

三红黑树特性

红黑树对于结点的颜色设置不是任意的，需满足以下性质的二叉查找树才是红黑树：
1.树中的每个结点颜色不是红的，就是黑的；
2.根结点的颜色是黑的；
3.所有为 nil 的叶子结点的颜色是黑的；（注意：叶子结点说的只是为空（nil 或 NULL）的叶子结点！）
4.如果此结点是红的，那么它的两个孩子结点全部都是黑的；
5.对于每个结点，从该结点到到该结点的所有子孙结点的所有路径上包含有相同数目的黑结点；

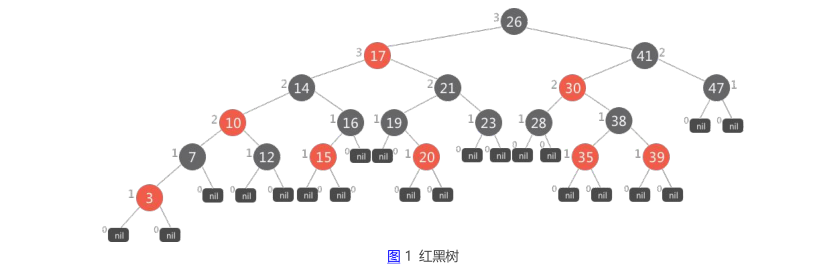
四红黑树图示

五红黑树高度

注意：图中每个结点附带一个整形数值，表示的是此结点的黑高度（从该结点到其子孙结点中包含的黑结点数，
用 bh(x) 表示（x 表示此结点）），nil 的黑高度为 0，颜色为黑色（在编程时为节省空间，
所有的 nil 共用一个存储空间）。在计算黑高度时，也看做是一个黑结点。

红黑树中每个结点都有各自的黑高度，整棵树也有自己的黑高度，即为根结点的黑高度，
例如图 1 中的红黑树的黑高度为 3。

对于一棵具有 n 个结点的红黑树，树的高度至多为：2lg(n+1)。

六时间复杂度

1
2
3

由此可推出红黑树进行查找操作时的时间复杂度为 O(lgn)，因为对于高度为 h 的二叉查找树的运行时间为 O(h)，
而包含有 n 个结点的红黑树本身就是最高为 lgn（简化之后）的查找树（h=lgn），
所以红黑树的时间复杂度为 O(lgn)。

七红黑树调整

红黑树本身作为一棵二叉查找树，所以其任务就是用于动态表中数据的插入和删除的操作。
在进行该操作时，避免不了会破坏红黑树的结构，此时就需要进行适当的调整，
使其重新成为一棵红黑树，可以从两个方面着手对树进行调整：
1.调整树中某些结点的指针结构；
2.调整树中某些结点的颜色；

八参考

C语言中文网—红黑树（更高级的二叉查找树）算法详解

0%