一 概述
1
2
3
4
| 1.行逻辑链接的顺序表
2.行逻辑链接的顺序表表示
3.提取稀疏矩阵元素过程
4.完整代码
|
二 行逻辑链接的顺序表
1
2
3
4
5
6
7
8
| 前面学习了如何使用三元组顺序表存储稀疏矩阵,其实现过程就是将矩阵中各个非 0 元素的行标、列标和元素值以三元组的形式存储到一维数组中。
通过研究实现代码你会发现,三元组顺序表每次提取指定元素都需要遍历整个数组,运行效率很低。
本节将学习另一种存储矩阵的方法——行逻辑链接的顺序表。它可以看作是三元组顺序表的升级版,即在三元组顺序表的基础上改善了提取数据的效率。
行逻辑链接的顺序表和三元组顺序表的实现过程类似,它们存储矩阵的过程完全相同,
都是将矩阵中非 0 元素的三元组(行标、列标和元素值)存储在一维数组中。
但为了提高提取数据的效率,前者在存储矩阵时比后者多使用了一个数组,专门记录矩阵中每行第一个非 0 元素在一维数组中的位置。
|
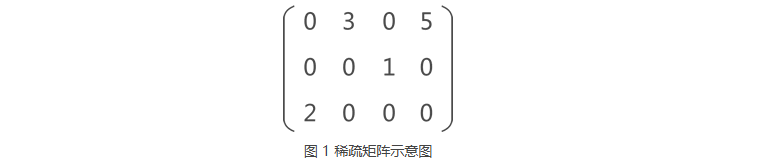
三 行逻辑链接的顺序表表示
图 1 是一个稀疏矩阵,当使用行逻辑链接的顺序表对其进行压缩存储时,需要做以下两个工作:
一、将矩阵中的非 0 元素采用三元组的形式存储到一维数组 data 中,如图 2 所示(和三元组顺序表一样)

二、使用数组 rpos 记录矩阵中每行第一个非 0 元素在一维数组中的存储位置。如图 3 所示

通过以上两步操作,即实现了使用行逻辑链接的顺序表存储稀疏矩阵。
四 提取稀疏矩阵元素过程
1
2
3
4
5
6
7
8
9
10
11
| 此时,如果想从行逻辑链接的顺序表中提取元素,则可以借助 rpos 数组提高遍历数组的效率。
例如,提取图 1 稀疏矩阵中的元素 2 的过程如下:
1.由 rpos 数组可知,第一行首个非 0 元素位于data[1],因此在遍历此行时,可以直接从第 data[1] 的位置开始,
一直遍历到下一行首个非 0 元素所在的位置(data[3])之前;
2.同样遍历第二行时,由 rpos 数组可知,此行首个非 0 元素位于 data[3],
因此可以直接从第 data[3] 开始,一直遍历到下一行首个非 0 元素所在的位置(data[4])之前;
3.遍历第三行时,由 rpos 数组可知,此行首个非 0 元素位于 data[4],由于这是矩阵的最后一行,
因此一直遍历到 rpos 数组结束即可(也就是 data[tu],tu 指的是矩阵非 0 元素的总个数)。
|
五 完整代码
5.1 以上操作的完整 C 语言实现代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
| #include <stdio.h>
#define MAXSIZE 12500
#define MAXRC 100
#define ElemType int
typedef struct
{
int i,j;//行,列
ElemType e;//元素值
}Triple;
typedef struct
{
Triple data[MAXSIZE+1];
int rpos[MAXRC+1];//每行第一个非零元素在data数组中的位置
int mu,nu,tu;//行数,列数,元素个数
}RLSMatrix;
//矩阵的输出函数
void display(RLSMatrix M){
for(int i=1;i<=M.mu;i++){
for(int j=1;j<=M.nu;j++){
int value=0;
if(i+1 <=M.mu){
for(int k=M.rpos[i];k<M.rpos[i+1];k++){
if(i == M.data[k].i && j == M.data[k].j){
printf("%d ",M.data[k].e);
value=1;
break;
}
}
if(value==0){
printf("0 ");
}
}else{
for(int k=M.rpos[i];k<=M.tu;k++){
if(i == M.data[k].i && j == M.data[k].j){
printf("%d ",M.data[k].e);
value=1;
break;
}
}
if(value==0){
printf("0 ");
}
}
}
printf("\n");
}
}
int main(int argc, char* argv[])
{
RLSMatrix M;
M.tu = 4;
M.mu = 3;
M.nu = 4;
M.rpos[1] = 1;
M.rpos[2] = 3;
M.rpos[3] = 4;
M.data[1].e = 3;
M.data[1].i = 1;
M.data[1].j = 2;
M.data[2].e = 5;
M.data[2].i = 1;
M.data[2].j = 4;
M.data[3].e = 1;
M.data[3].i = 2;
M.data[3].j = 3;
M.data[4].e = 2;
M.data[4].i = 3;
M.data[4].j = 1;
//输出矩阵
display(M);
return 0;
}
|
运行结果:
5.2 总结
1
2
| 通过系统地学习使用行逻辑链接的顺序表压缩存储稀疏矩阵,
可以发现,它仅比三元组顺序表多使用了一个 rpos 数组,从而提高了提取数据时遍历数组的效率。
|
六 参考


