数据结构与算法——第7章-图-普里姆算法(7.10.1)
一 概述
1 | 1.连通图的生成树 |
二 连通图的生成树
2.1 图示
1 | 通过前面的学习,对于含有 n 个顶点的连通图来说可能包含有多种生成树,例如图 1 所示: |
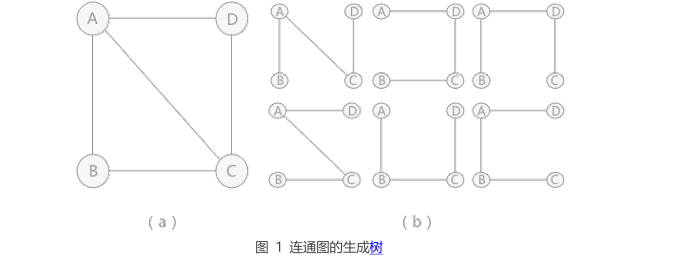
2.2 说明
1 | 图 1 中的连通图和它相对应的生成树,可以用于解决实际生活中的问题: |
三 权值
1 | 在具体选择采用(b)中哪一种方式时,需要综合考虑城市之间间隔的距离, |
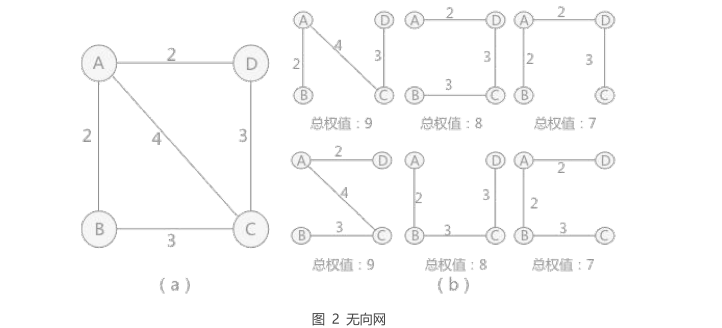
四 最小生成树
1 | 这就是本节要讨论的最小生成树的问题,简单得理解就是给定一个带有权值的连通图(连通网), |
五 参考
- C语言中文网—普里姆算法(Prim算法)求最小生成树