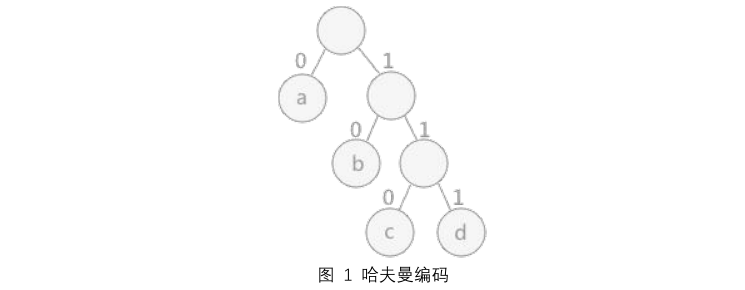
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
| #include<stdlib.h>
#include<stdio.h>
#include<string.h>
//哈夫曼树结点结构
typedef struct {
int weight;//结点权重
int parent, left, right;//父结点、左孩子、右孩子在数组中的位置下标
}HTNode, * HuffmanTree;
//动态二维数组,存储哈夫曼编码
typedef char** HuffmanCode;
//HT数组中存放的哈夫曼树,end表示HT数组中存放结点的最终位置,s1和s2传递的是HT数组中权重值最小的两个结点在数组中的位置
void Select(HuffmanTree HT, int end, int* s1, int* s2)
{
int min1, min2;
int i = 1, j;
//找到还没构建树的结点
while (HT[i].parent != 0 && i <= end) {
i++;
}
min1 = HT[i].weight;
*s1 = i;
i++;
while (HT[i].parent != 0 && i <= end) {
i++;
}
//对找到的两个结点比较大小,min2为大的,min1为小的
if (HT[i].weight < min1) {
min2 = min1;
*s2 = *s1;
min1 = HT[i].weight;
*s1 = i;
}
else {
min2 = HT[i].weight;
*s2 = i;
}
//两个结点和后续的所有未构建成树的结点做比较
for (j = i + 1; j <= end; j++)
{
//如果有父结点,直接跳过,进行下一个
if (HT[j].parent != 0) {
continue;
}
//如果比最小的还小,将min2=min1,min1赋值新的结点的下标
if (HT[j].weight < min1) {
min2 = min1;
min1 = HT[j].weight;
*s2 = *s1;
*s1 = j;
}
//如果介于两者之间,min2赋值为新的结点的位置下标
else if (HT[j].weight >= min1 && HT[j].weight < min2) {
min2 = HT[j].weight;
*s2 = j;
}
}
}
//HT为地址传递的存储哈夫曼树的数组,w为存储结点权重值的数组,n为结点个数
void CreateHuffmanTree(HuffmanTree* HT, int* w, int n)
{
int m, i;
if (n <= 1) return; // 如果只有一个编码就相当于0
m = 2 * n - 1; // 哈夫曼树总节点数,n就是叶子结点
*HT = (HuffmanTree)malloc((m + 1) * sizeof(HTNode)); // 0号位置不用
HuffmanTree p = *HT;
// 初始化哈夫曼树中的所有结点
for (i = 1; i <= n; i++)
{
(p + i)->weight = *(w + i - 1);
(p + i)->parent = 0;
(p + i)->left = 0;
(p + i)->right = 0;
}
//从树组的下标 n+1 开始初始化哈夫曼树中除叶子结点外的结点
for (i = n + 1; i <= m; i++)
{
(p + i)->weight = 0;
(p + i)->parent = 0;
(p + i)->left = 0;
(p + i)->right = 0;
}
//构建哈夫曼树
for (i = n + 1; i <= m; i++)
{
int s1, s2;
Select(*HT, i - 1, &s1, &s2);
(*HT)[s1].parent = (*HT)[s2].parent = i;
(*HT)[i].left = s1;
(*HT)[i].right = s2;
(*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
}
}
//HT为哈夫曼树,HC为存储结点哈夫曼编码的二维动态数组,n为结点的个数
void HuffmanCoding(HuffmanTree HT, HuffmanCode* HC, int n) {
int i, m, p, cdlen;
char* cd = NULL;
*HC = (HuffmanCode)malloc((n + 1) * sizeof(char*));
memset(*HC, NULL, n + 1);
m = 2 * n - 1;
p = m;
cdlen = 0;
cd = (char*)malloc(n * sizeof(char));
memset(cd, 0, n);
//将各个结点的权重用于记录访问结点的次数,首先初始化为0
for (i = 1; i <= m; i++) {
HT[i].weight = 0;
}
//一开始 p 初始化为 m,也就是从树根开始。一直到p为0
while (p) {
//如果当前结点一次没有访问,进入这个if语句
if (HT[p].weight == 0) {
HT[p].weight = 1;//重置访问次数为1
//如果有左孩子,则访问左孩子,并且存储走过的标记为0
if (HT[p].left != 0) {
p = HT[p].left;
cd[cdlen++] = '0';
}
//当前结点没有左孩子,也没有右孩子,说明为叶子结点,直接记录哈夫曼编码
else if (HT[p].right == 0) {
(*HC)[p] = (char*)malloc((cdlen + 1) * sizeof(char));
cd[cdlen] = '\0';
strcpy((*HC)[p], cd);
}
}
//如果weight为1,说明访问过一次,即是从其左孩子返回的
else if (HT[p].weight == 1) {
HT[p].weight = 2;//设置访问次数为2
//如果有右孩子,遍历右孩子,记录标记值 1
if (HT[p].right != 0) {
p = HT[p].right;
cd[cdlen++] = '1';
}
}
//如果访问次数为 2,说明左右孩子都遍历完了,返回父结点
else {
HT[p].weight = 0;
p = HT[p].parent;
--cdlen;
}
}
free(cd);
}
//打印哈夫曼编码的函数
void PrintHuffmanCode(HuffmanCode htable, int* w, int n)
{
printf("Huffman code : \n");
for (int i = 1; i <= n; i++) {
printf("%d code = %s\n", w[i - 1], htable[i]);
}
}
void DelHuffmanCode(HuffmanCode htable, int n) {
int i;
for (i = 0; i < n + 1; i++) {
if (htable[i]) {
free(htable[i]);
}
}
free(htable);
}
int main(void)
{
int w[5] = { 2, 8, 7, 6, 5 };
int n = 5;
HuffmanTree htree;
HuffmanCode htable;
CreateHuffmanTree(&htree, w, n);
HuffmanCoding(htree, &htable, n);
PrintHuffmanCode(htable, w, n);
//释放申请的堆内存
free(htree);
DelHuffmanCode(htable, n);
system("pause");
return 0;
}
|