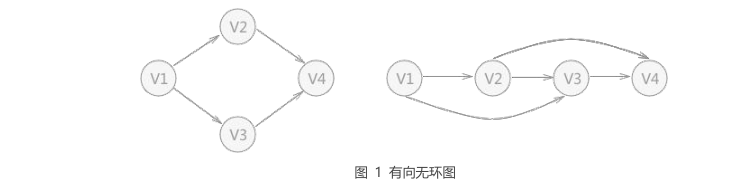
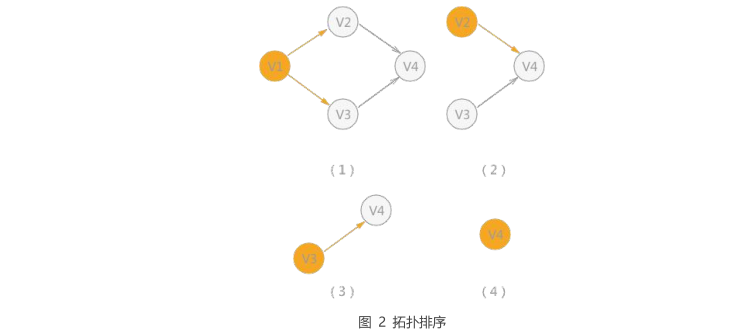
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
| #include <stdio.h>
#include <stdlib.h>
#define MAX_VERTEX_NUM 20//最大顶点个数
#define VertexType int//顶点数据的类型
typedef enum{false,true} bool;
typedef struct ArcNode{
int adjvex;//邻接点在数组中的位置下标
struct ArcNode * nextarc;//指向下一个邻接点的指针
}ArcNode;
typedef struct VNode{
VertexType data;//顶点的数据域
ArcNode * firstarc;//指向邻接点的指针
}VNode,AdjList[MAX_VERTEX_NUM];//存储各链表头结点的数组
typedef struct {
AdjList vertices;//图中顶点及各邻接点数组
int vexnum,arcnum;//记录图中顶点数和边或弧数
}ALGraph;
//找到顶点对应在邻接表数组中的位置下标
int LocateVex(ALGraph G,VertexType u){
for (int i=0; i<G.vexnum; i++) {
if (G.vertices[i].data==u) {
return i;
}
}
return -1;
}
//创建AOV网,构建邻接表
void CreateAOV(ALGraph **G){
*G=(ALGraph*)malloc(sizeof(ALGraph));
scanf("%d,%d",&((*G)->vexnum),&((*G)->arcnum));
for (int i=0; i<(*G)->vexnum; i++) {
scanf("%d",&((*G)->vertices[i].data));
(*G)->vertices[i].firstarc=NULL;
}
VertexType initial,end;
for (int i=0; i<(*G)->arcnum; i++) {
scanf("%d,%d",&initial,&end);
ArcNode *p=(ArcNode*)malloc(sizeof(ArcNode));
p->adjvex=LocateVex(*(*G), end);
p->nextarc=NULL;
int locate=LocateVex(*(*G), initial);
p->nextarc=(*G)->vertices[locate].firstarc;
(*G)->vertices[locate].firstarc=p;
}
}
//结构体定义栈结构
typedef struct stack{
VertexType data;
struct stack * next;
}stack;
//初始化栈结构
void initStack(stack* *S){
(*S)=(stack*)malloc(sizeof(stack));
(*S)->next=NULL;
}
//判断链表是否为空
bool StackEmpty(stack S){
if (S.next==NULL) {
return true;
}
return false;
}
//进栈,以头插法将新结点插入到链表中
void push(stack *S,VertexType u){
stack *p=(stack*)malloc(sizeof(stack));
p->data=u;
p->next=NULL;
p->next=S->next;
S->next=p;
}
//弹栈函数,删除链表首元结点的同时,释放该空间,并将该结点中的数据域通过地址传值给变量i;
void pop(stack *S,VertexType *i){
stack *p=S->next;
*i=p->data;
S->next=S->next->next;
free(p);
}
//统计各顶点的入度
void FindInDegree(ALGraph G,int indegree[]){
//初始化数组,默认初始值全部为0
for (int i=0; i<G.vexnum; i++) {
indegree[i]=0;
}
//遍历邻接表,根据各链表中结点的数据域存储的各顶点位置下标,在indegree数组相应位置+1
for (int i=0; i<G.vexnum; i++) {
ArcNode *p=G.vertices[i].firstarc;
while (p) {
indegree[p->adjvex]++;
p=p->nextarc;
}
}
}
void TopologicalSort(ALGraph G){
int indegree[G.vexnum];//创建记录各顶点入度的数组
FindInDegree(G,indegree);//统计各顶点的入度
//建立栈结构,程序中使用的是链表
stack *S;
initStack(&S);
//查找度为0的顶点,作为起始点
for (int i=0; i<G.vexnum; i++) {
if (!indegree[i]) {
push(S, i);
}
}
int count=0;
//当栈为空,说明排序完成
while (!StackEmpty(*S)) {
int index;
//弹栈,并记录栈中保存的顶点所在邻接表数组中的位置
pop(S,&index);
printf("%d",G.vertices[index].data);
++count;
//依次查找跟该顶点相链接的顶点,如果初始入度为1,当删除前一个顶点后,该顶点入度为0
for (ArcNode *p=G.vertices[index].firstarc; p; p=p->nextarc) {
VertexType k=p->adjvex;
if (!(--indegree[k])) {
//顶点入度为0,入栈
push(S, k);
}
}
}
//如果count值小于顶点数量,表明该有向图有环
if (count<G.vexnum) {
printf("该图有回路");
return;
}
}
int main(){
ALGraph *G;
CreateAOV(&G);//创建AOV网
TopologicalSort(*G);//进行拓扑排序
return 0;
}
|