一 概述
1
2
3
| 本文详细介绍了C语言中顺序表的实现,
包括顺序表的结构、如何动态申请存储空间、插入元素到不同位置的方法、删除元素、查找元素以及更改元素的操作。
通过实例展示了完整的代码实现过程
|
二 顺序表(顺序存储结构)
2.1 概念
1
2
3
4
5
6
7
| 顺序表(顺序存储结构)是线性表的一种。
顺序表对数据的物理存储结构也有要求:
顺序表存储数据时,会提前申请一整块足够大小的物理空间,
然后将数据依次存储起来,存储时做到数据元素之间不留一丝缝隙。
使用顺序表存储集合{1,2,3,4,5},数据最终的存储状态如下
|
图示

2.2 顺序表物理存储
1
2
3
4
5
6
7
| 顺序存储结构将具有“一对一”逻辑关系的数据按次序连续存储到一整块物理空间上。
其实,顺序表存储数据使用的就是数组。
使用顺序表存储数据之前,除了要申请足够大小的物理空间外,
为了方便后期使用表中的数据,顺序表还要实时记录以下 2 项数据:
-顺序表申请的存储容量(正常状态下,顺序表申请的存储容量要大于顺序表的长度)
-顺序表的长度(即表中存储数据元素的个数)
|
2.3 C 语言自定义顺序表
1
2
3
4
5
6
7
8
9
10
| typedef struct Table{
int * head; // 声明了一个名为 head 的长度不确定的数组, 也叫 “动态数组”
int length; // 记录当前顺序表的长度
int size; // 记录顺序表分配的存储容量
} table;
head 是我们声明的一个未初始化的动态数组,不要只把它看做是普通的指针。
建立顺序表(顺序表的初始化)需做如下工作:
-给 head 动态数据申请足够大小的物理空间
-给 size 和 length 赋初值
|
2.4 C 语言实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| // 对 Size 进行宏定义, 表示顺序表申请空间的大小
#define Size 5
table initTable(){
table t;
// 构造一个空的顺序表, 动态申请存储空间
t.head = (int*)malloc(Size*sizeof(int));
// 如果申请失败, 作出提示并直接退出程序
if (!t.head)
{
printf("初始化失败");
exit(0);
}
t.length=0; // 空表的长度初始化为 0
t.size=Size; // 空表的初始存储空间为 Size
return t;
}
|
2.5 C语言完整示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| 整个顺序表初始化的过程被封装到了一个函数中,此函数返回值是一个已初始化完成的顺序表。
顺序表初始化过程中,要注意对物理空间的申请进行判断,对申请失败的情况进行处理,
这里只进行了“输出提示信息和强制退出”的操作,可以根据自己的需要对代码中的 if 语句进行改进。
通过在主函数中调用 initTable 语句,就可以成功创建一个空的顺序表,与此同时还可以试着向顺序表中添加一些元素:
#include <stdio.h>
#include <stdlib.h>
#define Size 5
typedef struct Table{
int * head;
int length;
int size;
}table;
table initTable(){
table t;
t.head=(int*)malloc(Size*sizeof(int));
if (!t.head)
{
printf("初始化失败");
exit(0);
}
t.length=0;
t.size=Size;
return t;
}
// 输出顺序表中元素的函数
void displayTable(table t){
for (int i=0;i<t.length;i++) {
printf("%d ",t.head[i]);
}
printf("\n");
}
int main(){
table t=initTable();
// 向顺序表中添加元素
for (int i=1; i<=Size; i++) {
t.head[i-1]=i;
t.length++;
}
printf("顺序表中存储的元素分别是:\n");
displayTable(t);
return 0;
}
/*
顺序表中存储的元素分别是:
1 2 3 4 5
*/
|
三 顺序表的基本操作
3.1 插入元素
一、概念
1
2
3
4
5
6
7
8
9
| 向已有顺序表中插入数据元素,根据插入位置的不同,可分为以下 3 种情况:
-插入到顺序表的表头
-在表的中间位置插入元素
-尾随顺序表中已有元素,作为顺序表中的最后一个元素
虽然数据元素插入顺序表中的位置有所不同,但都使用的是同一种方式去解决:
通过遍历,找到数据元素要插入的位置,然后做如下两步工作:
-将要插入位置元素以及后续的元素整体向后移动一个位置
-将元素放到腾出来的位置上
|
二、示例:例如,在{1,2,3,4,5}的第 3 个位置上插入元素 6
2-1 遍历至顺序表存储第 3 个数据元素的位置
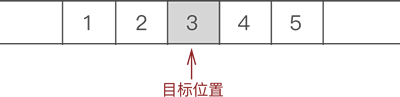
2-2 将元素 3 以及后续元素 4 和 5 整体向后移动一个位置:
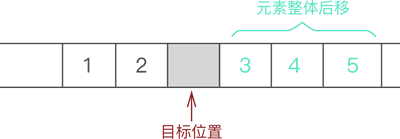
2-3 将新元素 6 放入腾出的位置
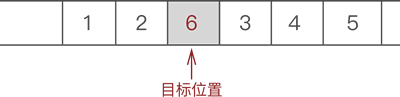
三、顺序表插入数据元素的 C 语言实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| // 插入函数, elem 为插入的元素, add 为插入到顺序表的位置
table addTable(table t,int elem,int add)
{
// 判断插入本身是否存在问题(如果插入元素位置比整张表的长度 +1 还大(如果相等, 是尾随的
// 情况), 或插入的位置本身不存在, 程序作为提示并自动退出)
if (add>t.length+1||add<1) {
printf("插入位置有问题\n");
return t;
}
// 做插入操作时, 首先需要看顺序表是否有多余的存储空间提供给插入的元素, 如果没有, 需要申请
if (t.length==t.size) {
t.head=(int *)realloc(t.head, (t.size+1)*sizeof(int));
if (!t.head) {
printf("存储分配失败\n");
return t;
}
t.size+=1;
}
// 插入操作, 需要将从插入位置开始的后续元素, 逐个后移
for (int i=t.length-1; i>=add-1; i--) {
t.head[i+1]=t.head[i];
}
// 后移完成后, 直接将所需插入元素, 添加到顺序表的相应位置
t.head[add-1]=elem;
// 由于添加了元素, 所以长度+1
t.length++;
return t;
}
|
注意:
- 动态数组额外申请更多物理空间使用的是 realloc 函数。
- 在实现后续元素整体后移的过程,目标位置其实是有数据的,
- 还是 3,只是下一步新插入元素时会把旧元素直接覆盖。
3.2 删除元素
一、说明
1
2
3
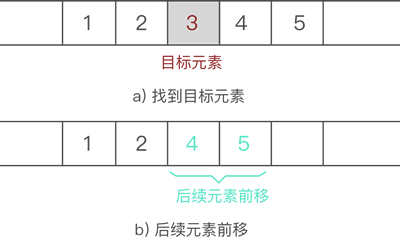
| 从顺序表中删除指定元素,实现起来非常简单,只需找到目标元素,并将后续所有元素整体前移 1 个位置即可。
后续元素整体前移一个位置,会直接将目标元素删除,可间接实现删除元素的目的。
从{1,2,3,4,5}中删除元素 3:
|
图示
二、顺序表删除元素的 C 语言实现
1
2
3
4
5
6
7
8
9
10
11
12
| table delTable(table t,int add){
if (add>t.length || add<1) {
printf("被删除元素的位置有误\n");
return t;
}
// 删除操作
for (int i=add; i<t.length; i++) {
t.head[i-1]=t.head[i];
}
t.length--;
return t;
}
|
3.3 查找元素
1
2
3
4
5
6
7
8
9
10
11
12
| 顺序表中查找目标元素,可以使用多种查找算法实现,比如二分查找等。以下选择顺序查找算法
// 查找函数, elem 表示要查找的数据元素的值
int selectTable(table t,int elem){
for (int i=0; i<t.length; i++) {
if (t.head[i]==elem) {
return i+1;
}
}
// 如果查找失败, 返回-1
return -1;
}
|
3.4 更改元素
一、顺序表更改元素的实现过程
二、顺序表更改元素(C 语言实现)
1
2
3
4
5
6
7
| // 更改函数, elem 为要更改的元素, newElem 为新的数据元素
table amendTable(table t,int elem,int newElem){
int add=selectTable(t, elem);
// 由于返回的是元素在顺序表中的位置, 所以 -1 就是该元素在数组中的下标
t.head[add-1]=newElem;
return t;
}
|
四 顺序表基本操作(完整实现代码)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
| #include <stdio.h>
#include <stdlib.h>
#define Size 5
typedef struct Table{
int * head;
int length;
int size;
}table;
table initTable(){
table t;
t.head=(int*)malloc(Size*sizeof(int));
if (!t.head)
{
printf("初始化失败\n");
exit(0);
}
t.length=0;
t.size=Size;
return t;
}
table addTable(table t,int elem,int add)
{
if (add>t.length+1||add<1) {
printf("插入位置有问题\n");
return t;
}
if (t.length>=t.size) {
t.head=(int *)realloc(t.head, (t.size+1)*sizeof(int));
if (!t.head) {
printf("存储分配失败\n");
}
t.size+=1;
}
for (int i=t.length-1; i>=add-1; i--) {
t.head[i+1]=t.head[i];
}
t.head[add-1]=elem;
t.length++;
return t;
}
table delTable(table t,int add){
if (add>t.length || add<1) {
printf("被删除元素的位置有误\n");
return t;
}
for (int i=add; i<t.length; i++) {
t.head[i-1]=t.head[i];
}
t.length--;
return t;
}
int selectTable(table t,int elem){
for (int i=0; i<t.length; i++) {
if (t.head[i]==elem) {
return i+1;
}
}
return -1;
}
table amendTable(table t,int elem,int newElem){
int add=selectTable(t, elem);
t.head[add-1]=newElem;
return t;
}
void displayTable(table t){
for (int i=0;i<t.length;i++) {
printf("%d ",t.head[i]);
}
printf("\n");
}
int main(){
table t1=initTable();
for (int i=1; i<=Size; i++) {
t1.head[i-1]=i;
t1.length++;
}
printf("原顺序表:\n");
displayTable(t1);
printf("删除元素1:\n");
t1=delTable(t1, 1);
displayTable(t1);
printf("在第2的位置插入元素5:\n");
t1=addTable(t1, 5, 2);
displayTable(t1);
printf("查找元素3的位置:\n");
int add=selectTable(t1, 3);
printf("%d\n",add);
printf("将元素3改为6:\n");
t1=amendTable(t1, 3, 6);
displayTable(t1);
return 0;
}
/*
原顺序表:
1 2 3 4 5
删除元素1:
2 3 4 5
在第2的位置插入元素5:
2 5 3 4 5
查找元素3的位置:
3
将元素3改为6:
2 5 6 4 5
*/
|
五 参考




