一 概述
1
2
3
| 1.2-路插入排序算法
2.2-路插入排序算法图示
3.示例代码
|
二 2-路插入排序算法
1
2
3
4
5
6
7
8
| 2-路插入排序算法是在折半插入排序的基础上对其进行改进,减少其在排序过程中移动记录的次数从而提高效率。
具体实现思路为:
另外设置一个同存储记录的数组大小相同的数组 d,将无序表中第一个记录添加进 d[0] 的位置上,然
后从无序表中第二个记录开始,同 d[0] 作比较:
如果该值比 d[0] 大,则添加到其右侧;反之添加到其左侧。
在这里的数组 d 可以理解成一个环状数组。
|
三 2-路插入排序算法图示
使用 2-路插入排序算法对无序表{3,1,7,5,2,4,9,6}排序的过程如下:
一、步骤1
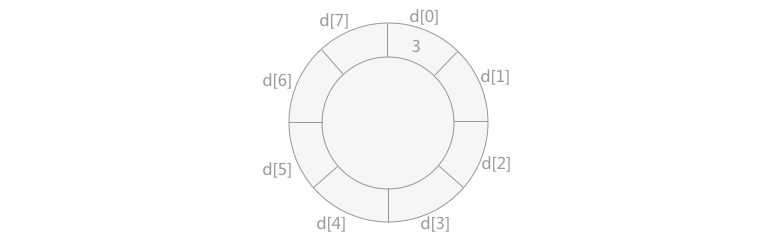
二、步骤2
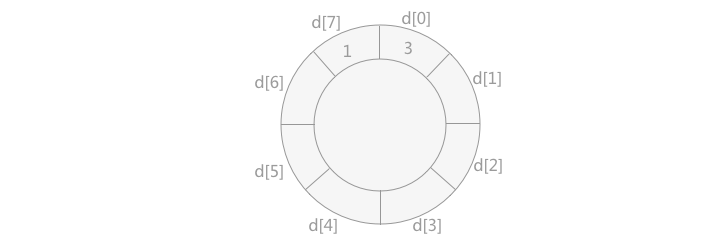
三、步骤3
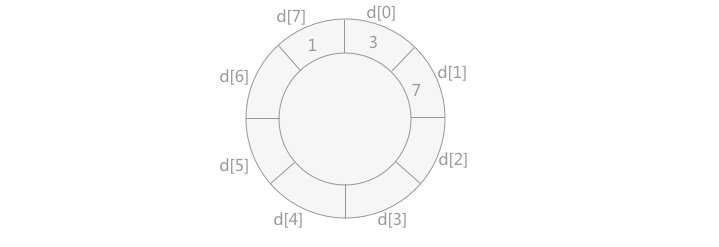
四、步骤4
1
| 将记录 5 插入到数组 d 中,由于其比 7小,但是比 3 大,所以需要移动 7 的位置,然后将 5 插入,如下图所示:
|
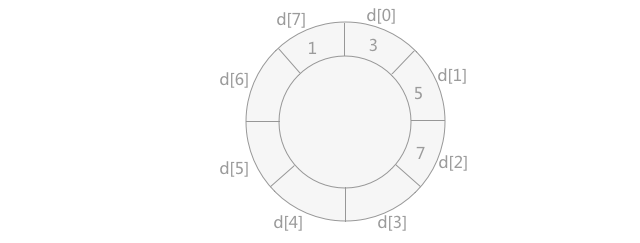
五、步骤5
1
| 将记录 2 插入到数组 d 中,由于比 1大,比 3 小,所以需要移动 3、7、5 的位置,然后将 2 插入,如下图所示:
|
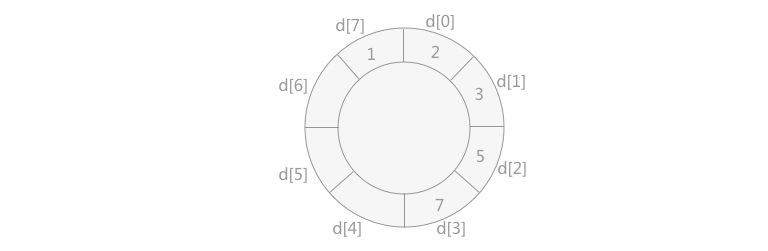
六,步骤6
1
| 将记录 4 插入到数组 d 中,需要移动 5 和 7 的位置,如下图所示:
|
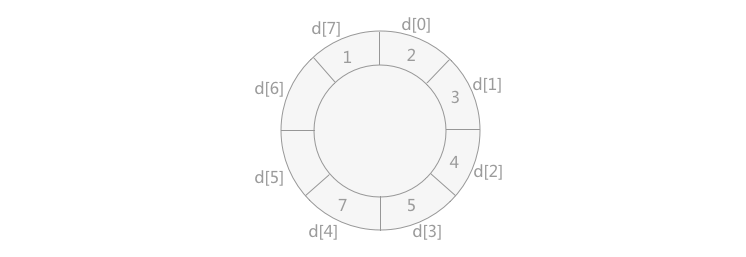
七、步骤7
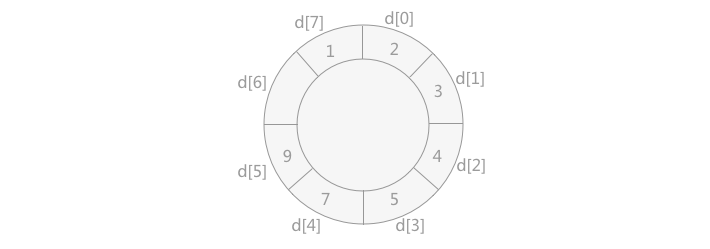
八、步骤8
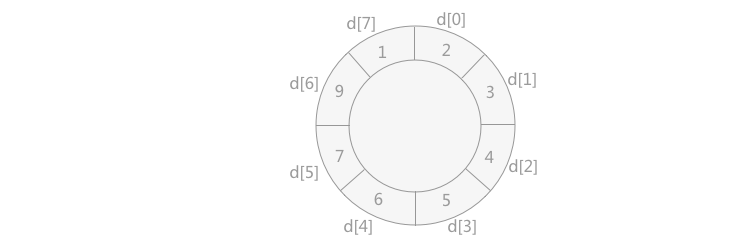
最终存储在原数组时,从 d7 开始依次存储。
四 示例代码
4.1 2-路插入排序算法的具体实现代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include <stdio.h>
#include <stdlib.h>
void insert(int arr[], int temp[], int n)
{
int i,first,final,k;
first = final = 0;//分别记录temp数组中最大值和最小值的位置
temp[0] = arr[0];
for (i = 1; i < n; i ++){
// 待插入元素比最小的元素小
if (arr[i] < temp[first]){
first = (first - 1 + n) % n;
temp[first] = arr[i];
}
// 待插入元素比最大元素大
else if (arr[i] > temp[final]){
final = (final + 1 + n) % n;
temp[final] = arr[i];
}
// 插入元素比最小大,比最大小
else {
k = (final + 1 + n) % n;
//当插入值比当前值小时,需要移动当前值的位置
while (temp[((k - 1) + n) % n] > arr[i]) {
temp[(k + n) % n] =temp[(k - 1 + n) % n];
k = (k - 1 + n) % n;
}
//插入该值
temp[(k + n) % n] = arr[i];
//因为最大值的位置改变,所以需要实时更新final的位置
final = (final + 1 + n) % n;
}
}
// 将排序记录复制到原来的顺序表里
for (k = 0; k < n; k ++) {
arr[k] = temp[(first + k) % n];
}
}
int main()
{
int a[8] = {3,1,7,5,2,4,9,6};
int temp[8];
insert(a,temp,8);
for (int i = 0; i < 8; i ++){
printf("%d ", a[i]);
}
return 0;
}
|
4.2 运行结果为:
4.3 时间复杂度
1
| 2-路插入排序相比于折半插入排序,只是减少了移动记录的次数,没有根本上避免,所以其时间复杂度仍为O(n2)。
|
五 参考







