数据结构与算法——第5章-数组和广义表-矩阵乘法(5.9.1)

发表于 分类于 ， ， 阅读时长 ≈ 1 分钟

一 概述

1
2
3
1.矩阵乘法
2.矩阵乘法图示
3.示例代码

二 矩阵乘法

1
2
矩阵相乘的前提条件是：乘号前的矩阵的列数要和乘号后的矩阵的行数相等。
且矩阵的乘法运算没有交换律，即 A*B 和 B*A 是不一样的。

三 矩阵乘法图示

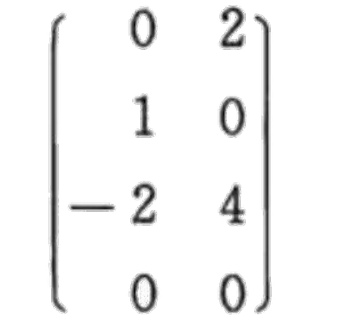
3.1 矩阵A和矩阵B

矩阵A 矩阵B

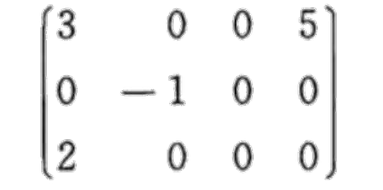3.2 矩阵乘法

1
2
3
4
5
6
7
由于矩阵 A 的列数和矩阵 B 的行数相等，可以进行 A*B 运算（不能进行 B*A 运算）。
计算方法是：用矩阵 A 的第 i 行和矩阵 B 中的每一列 j 对应的数值做乘法运算，乘积一一相加，所得结果即为矩阵 C 中第 i 行第 j 列的值。
得到的乘积矩阵 C 为：

例如：C 12 = 6 是因为：A 11 *B 12 + A 12 *B 22 + A 13 *B 32 + A 14 *B 42 ，即 3*2 + 0*0 + 0*4 + 5*0 = 6 ，
因为这是 A 的第 1 行和 B 的第 2 列的乘积和，
所以结果放在 C 的第 1 行第 2 列的位置。

四 示例代码

4.1 说明

1
例如，A 是 m1*n1 矩阵，B 是 m2*n2 矩阵(前提必须是 n1 == m2 )：

4.2 代码

1
2
3
4
5
6
7
8
9
int C[MAX][MAX];
for (int i=0; i<m1; i++) {
	for (int j=0; j<n2; j++) {
		C[i][j]=0;
		for (int k=0; k<n1; k++) {
			C[i][j]+=A[i][k]*B[k][j];
		}
	}
}

4.3 说明

1
2
普通算法的时间复杂度为 O(m1*n2*n1)。
在稀疏矩阵做乘法运算时，由于本身矩阵中含有的非 0 元素少，普通算法会出现很多 0*0 或者 k*0 或者 0*k （ k 代表非 0 元素值）的情况。下面介绍使用行逻辑链接的顺序表计算矩阵乘积的方法。

五 参考

  • C语言中文网—行逻辑链接的顺序表实现矩阵乘法