一 概述
1
2
3
| 1.查找关键字所在结点
2.该结点为最后一层的非终端结点情况
3.总结
|
二 查找关键字所在结点
1
2
3
4
5
6
7
8
9
10
11
| 在 B-树种删除关键字时,首先前提是找到该关键字所在结点,在做删除操作的时候分为两种情况,
一种情况是删除结点为 B-树的非终端结点(不处在最后一层);
另一种情况是删除结点为 B-树最后一层的非终端结点。
例如图 3 来说,关键字 24、45、53、90 属于不处在最后一层的非终端结点,
关键字 3、12、37 等同属于最后一层的非终端结点。
如果该结点为非终端结点且不处在最后一层,假设用 K i 表示,
则只需要找到指针 A i 所指子树中最小的一个关键字代替 K i ,同时将该最小的关键字删除即可。
例如图 3 中,如果要删除关键字 45 ,只需要使用关键字 50 代替 45 ,同时删除 f 结点中的 50 即可。
|
三 该结点为最后一层的非终端结点情况
如果该结点为最后一层的非终端结点,有下列 3 种可能
一、情况1
1
2
| 被删关键字所在结点中的关键字数目不小于⌈ m/2⌉ ,则只需从该结点删除该关键字 K i 以及相应的指针 A i 。
例如,在图 3 中,删除关键字 12 ,只需要删除该关键字 12 以及右侧指向 NULL 指针即可。
|
二、情况2
1
2
3
4
| 被删关键字所在结点中的关键字数目等于⌈ m/2⌉ -1,
而与该结点相邻的右兄弟结点(或者左兄弟)结点中的关键字数目大于⌈ m/2⌉ -1,
只需将该兄弟结点中的最小(或者最大)的关键字上移到双亲结点中,
然后将双亲结点中小于(或者大于)且紧靠该上移关键字的关键字移动到被删关键字所在的结点中。
|
1
2
3
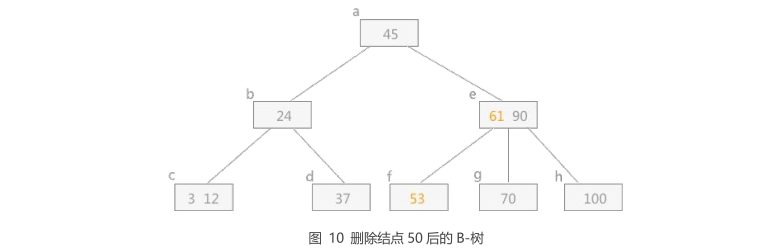
| 例如在图 3 中删除关键字 50,其右兄弟结点 g 中的关键字大于 2,
所以需要将结点 g 中最小的关键字 61 上移到其双亲结点 e 中(由此 e中结点有:53,61,90),
然后将小于 61 且紧靠 61 的关键字 53 下移到结点 f 中,最终删除后的 B-树如图 10 所示。
|
三、情况3
1
2
3
4
5
6
7
| 被删除关键字所在的结点如果和其相邻的兄弟结点中的关键字数目都正好等于⌈ m/2⌉ -1,
假设其有右兄弟结点,且其右兄弟结点是由双亲结点中的指针 A i 所指,则需要在删除该关键字的同时,
将剩余的关键字和指针连同双亲结点中的 K i 一起合并到右兄弟结点中。
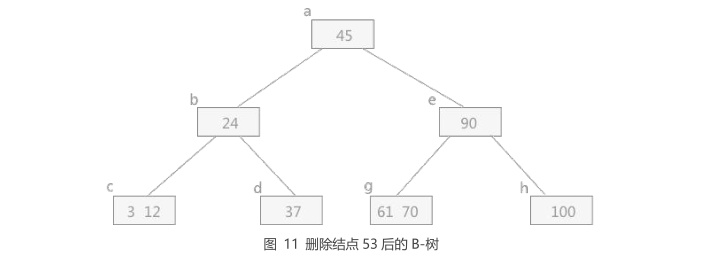
例如,在图 10 中 B-树中删除关键字 53,由于其有右兄弟,且右兄弟结点中只有 1 个关键字。在删除关键字 53 后,
结点 f 中只剩指向叶子结点的空指针,
连同双亲结点中的 61(因为 61 右侧指针指向的兄弟结点 g)一同合并到结点 g 中,最终删除 53 后的 B-树为:
|
1
2
3
4
5
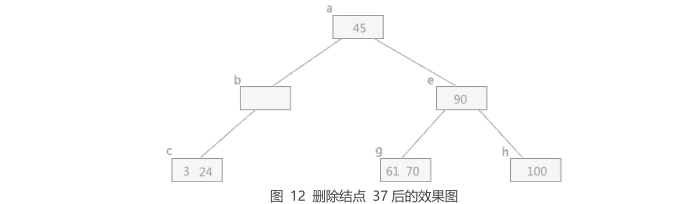
| 在合并的同时,由于从双亲结点中删除一个关键字,若导致双亲结点中关键字数目小于⌈ m/2⌉ -1,
则继续按照该规律进行合并。例如在图 11中 B-树的情况下删除关键字 12 时,结点 c 中只有一个关键字,
然后做删除关键字 37 的操作。
此时在删除关键字 37 的同时,结点 d 中的剩余信息(空指针)同双亲结点中的关键字 24 一同合并到结点 c 中,
效果图为:
|
1
2
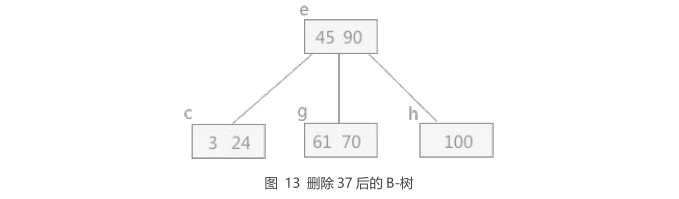
| 由于结点 b 中一个关键字也没有,所以破坏了 B-树的结构,继续整合。在删除结点 b 的同时,
由于 b 中仅剩指向结点 c 的指针,所以连同其双亲结点中的 45 一同合并到其兄弟结点 e 中,最终的 B-树为:
|
四 总结
1
2
| 由于 B-树具有分支多层数少的特点,使得它更多的是应用在数据库系统中。
除了 B-树,还有专门为文件系统而生的 B+树,在本章的下一节会详细介绍。
|
五 参考



