数据结构与算法——第9章-查找表-B-树中插入关键字(9.9.2)

发表于 分类于 ， ， 阅读时长 ≈ 1 分钟

一 概述

1
2
3
1.B-树插入数据
2.插入数据演示
3.总结

二 B-树插入数据

1
2
3
4
5
6
7
8
B-树也是从空树开始，通过不断地插入新的数据元素构建的。
但是 B-树构建的过程同前面章节的二叉排序树和平衡二叉树不同，
B-树在插入新的数据元素时并不是每次都向树中插入新的结点。

因为对于 m 阶的 B-树来说，在定义中规定所有的非终端结点
（终端结点即叶子结点，其关键字个数为 0）中包含关键字的个数的范围是[⌈ m/2⌉-1,m-1]，
所以在插入新的数据元素时，首先向最底层的某个非终端结点中添加，如果该结点中的关键字个数没有超过 m-1，
则直接插入成功，否则还需要继续对该结点进行处理。

三 插入数据演示

3.1 B-树

1
假设现在图 3 的基础上插入 4 个关键字 30、26、85 和 7：

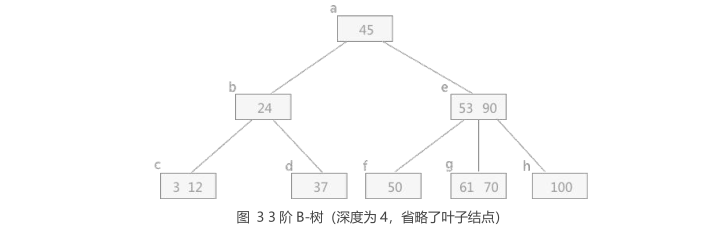
3.2 过程演示

一、插入关键字 30

1
2
3
从根结点开始，由于 30 < 45，所以要插入到以 b 结点为根结点的子树中，
再由于 24 < 30，插入到以 d 结点为根结点的子树中，
由于 d 结点中的关键字个数小于 m-1=2，所以可以将关键字 30 直接插入到 d 结点中。结果如下图所示：

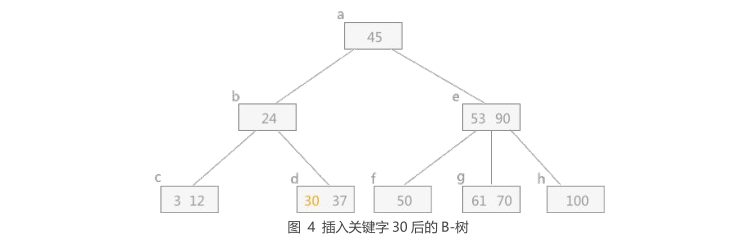
二、插入关键字 26

1
2
3
4
5
从根结点开始，经过逐个比较，最终判定 26 还是插入到 d 结点中，但是由于 d 结点中关键字的个数超过了 2，
所以需要做如下操作：
1.关键字 37 及其左右两个指针存储到新的结点中，假设为 d’ 结点；
2.关键字 30 存储到其双亲结点 b 中，同时设置关键字 30 右侧的指针指向 d’；
经过以上操作后，插入 26 后的 B-树为：

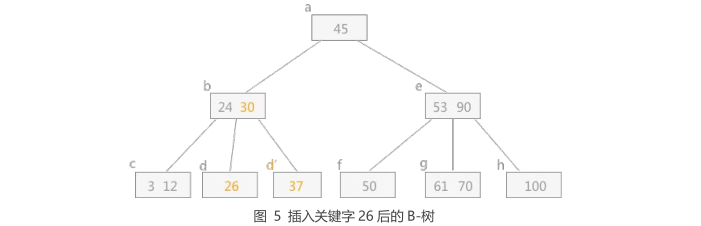
三、插入关键字 85

1
2
3
4
从根结点开始，经过逐个比较，最终判定插入到 g 结点中，同样需要对 g 做分裂操作：
1.关键字 85 及其左右两个指针存储到新的结点中，假设为 g’ 结点；
2.关键字 70 存储到其双亲结点 e 中，同时设置 70 的右侧指针指向 g’ ；
经过以上操作后，插入 85 后的结果图为：

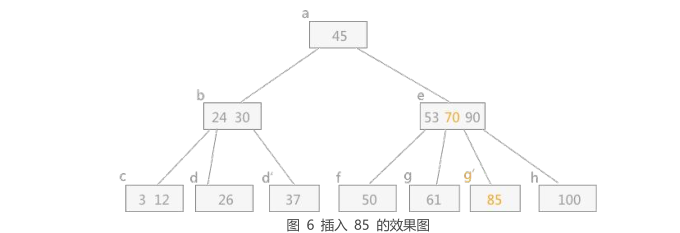
四、插入关键字 85

1
2
3
4
图 6 中，由于关键字 70 调整到其双亲结点中，使得其 e 结点中的关键字个数超过了 2，所以还需进一步调整：
1.将 90 及其左右指针存储到一个新的结点中，假设为 e’ 结点；
2.关键字 70 存储到其双亲结点 a 中，同时其右侧指针指向 e’ ;
最终插入关键字 85 后的 B-树为：

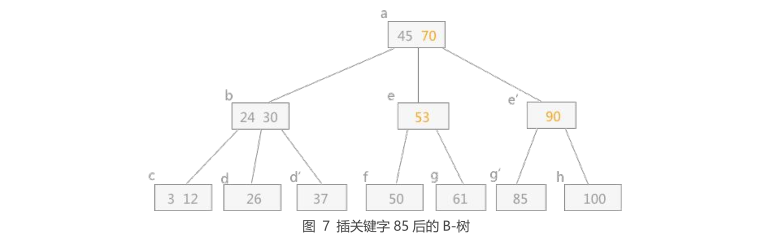
五、插入关键字 7

1
2
3
4
从根结点开始依次做判断，最终判定在 c 结点中添加，添加后发现 c 结点需要分裂，分裂规则同上面的方式一样，
结果导致关键字 7存储到其双亲结点 b 中；
后 b 结点分裂，关键字 24 存储到结点 a 中；
结点 a 同样需要做分裂操作，最终 B-树为：

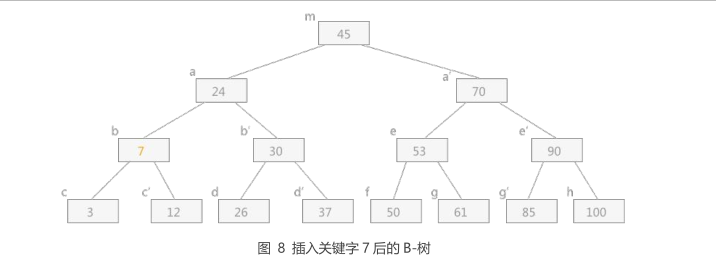
四 总结

1
2
通过上边的例子，可以总结出一下结论：在构建 B-树的过程中，
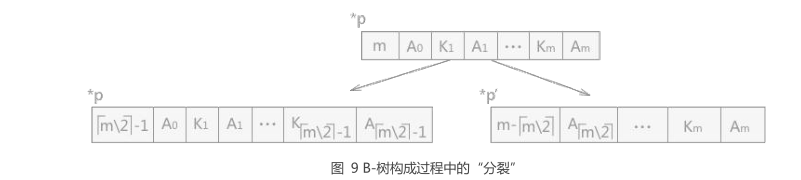
假设 p 结点中已经有 m-1 个关键字，当再插入一个关键字之后，此结点分裂为两个结点，如下图所示：

1
提示：如图 9 所示，结点分裂为两个结点的同时，还分裂出来一个关键字 K ⌈ m/2⌉ ，存储到其双亲结点中。

五 参考

  • C语言中文网—B-树及其基本操作