数据结构与算法——第5章-数组和广义表-十字链表(5.10.2)

发表于 2023-03-05 分类于开发， N-数据与算法，数据结构与算法阅读时长 ≈ 1 分钟

一概述

1.十字链表法
2.十字链表法表示矩阵
3.十字链表中的结点
4.十字链表的结构

之前所介绍的都是采用顺序存储结构存储三元组，在类似于矩阵的加法运算中，矩阵中的数据元素变化较大
（这里的变化主要为：非 0 元素变为 0，0变为非 0 元素），就需要考虑采用另一种结构——链式存储结构来存储三元组。

采用链式存储结构存储稀疏矩阵三元组的方法，称为“十字链表法”。

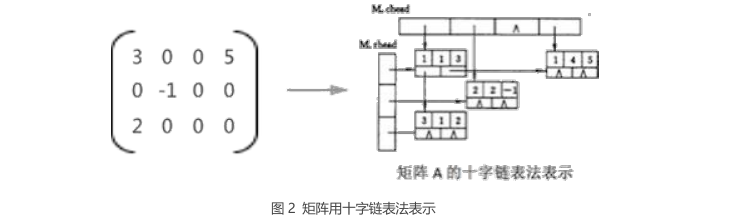
1	例如，用十字链表法表示矩阵 A ，为：

由此可见，采用十字链表表示矩阵时，矩阵的每一行和每一个列都可以看作是一个单独的链表，
而之所以能够表示矩阵，是因为行链表和列链表都分别存储在各自的数组中

图 2 中：存储行链表的数组称为 rhead 数组；存储列链表的数组称为 chead 数组。

1
2
3

从图 2 中的十字链表表示矩阵的例子可以看到，十字链表中的结点由 5 部分组成：
指针域 A 存储的是矩阵中结点所在列的下一个结点的地址（称为 “down 域”）；
指针域 B 存储的是矩阵中该结点所在行的下一个结点的地址（称为 “right 域”）；

typedef struct OLNode {
	int i,j,e; //矩阵三元组 i 代表行 j 代表列 e 代表当前位置的数据
	struct OLNode *right,*down; //指针域 右指针 下指针
} OLNode,*OLink;

1
2

使用十字链表表示一个完整的矩阵，在了解矩阵中各结点的结构外，还需要存储矩阵的行数、列数以及非 0 元素的个数，
另外，还需要将各结点链接成的链表存储在数组中。

所以，采用结构体自定义十字链表的结构，为：

typedef struct {
	OLink *rhead,*chead; //存放各行和列链表头指针的数组
	int mu,nu,tu; //矩阵的行数,列数和非零元的个数
} CrossList;