一 概述
1
2
3
4
| 1.数据的存储
2.常用数据结构
3.数据的逻辑结构、存储结构(物理结构)
4.数据结构和算法的关系和区别
|
二 数据的存储
2.1 数据存储目的
1
2
3
4
5
| 数据结构主要研究数据的存储方式。
数据存储的目的:
方便后期对数据的再利用。数据在计算机存储空间的存放是有讲究的,
这就要求我们选择一种好的方式来存储数据,这也是数据结构的核心。
|
2.2 简单存储
1
2
3
4
5
6
7
| 例如,大家要存储的数据大多类似1、2、{a,b,c}、"yuque.com/it-coach/dsure"这样的数据,
解决方式无疑是用变量或数组对数据进行存储:
int a=1;
int b=2;
char str[3]={'a','b','c'};
char *data="yuque.com/it-coach/dsure";
|
2.3 复杂存储
1
2
| 但如果要存储这样一组数据:`{张亮,张平,张华,张群,张晶,张磊}`,
数据之间有如下关系(张亮是张平、张华和张群的父亲,同时张平还是张晶和张磊的父亲):
|
图示
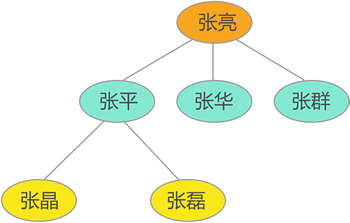
如何存储
1
2
3
4
5
6
7
8
| 对于具有复杂关系的数据,如果还是用变量或数组来存储
(比如用数组存储{“张亮”,"张平",“张华”,"张群","张晶","张磊"}),
则无法体现数据之间的逻辑关系,后期根本无法使用。
数据结构中提供有专门的树结构来存储这类数据。
再比如,导航软件的导航功能的实现都需要大量地图数据的支持,
这些数据绝不是使用变量或数组进行存储的,那样对于数据的使用简直是个悲剧。
数据结构提供了图存储结构专门用于存储这类数据。
|
数据结构教会我们解决具有复杂关系的大量数据的存储问题。数据结构是一门学科
三 常用数据结构
3.1 线性表
1
2
3
4
5
| 线性表结构存储的数据往往是可依次排列的。
例如,存储类似{1,3,5,7,9}这样的数据时,各元素依次排列,
每个元素的前面和后边有且仅有一个元素与之相邻(除首元素和尾元素)。
线性表并不是一种具体的存储结构,它包含顺序存储结构和链式存储结构,是顺序表和链表的统称。
|
3.1.1 顺序表
1
2
3
4
5
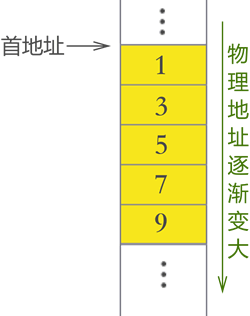
| 顺序表,简单理解就是常用的数组,例如使用顺序表存储{1,3,5,7,9}
顺序表结构的底层实现借助的是数组,初学者可以把顺序表完全等价为数组,
但实则不是这样(数据结构是研究数据存储方式的一门学科,
它囊括各种存储结构,而数组只是各种编程语言中的基本数据类型,并不属于数据结构的范畴)。
|
图示
3.1.2 链表
1
2
3
4
5
6
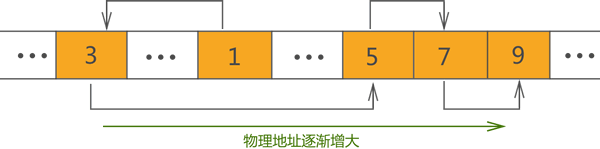
| 使用顺序表(底层靠数组实现)时需提前申请一定大小的存储空间,这块存储空间的物理地址是连续的。
使用链表存储数据时,是随用随申请,因此数据的存储位置是相互分离的(数据的存储位置是随机的)。
为了给各个数据块建立“依次排列”的关系,链表给各数据块增设一个指针,
每个数据块的指针都指向下一个数据块(最后一个数据块的指针指向NULL):
|
图示
3.1.3 栈和队列
栈和队列是特殊的线性表,它们对线性表中元素的进出做了明确的要求。
栈
1
2
3
4
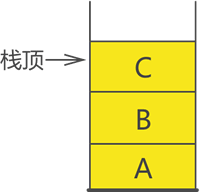
| 栈中的元素只能从线性表的一端进出(另一端封死),遵循“先入后出”原则(先进栈的元素后出栈)
栈结构像一个木桶,栈中含有 3 个元素:A、B 和 C,从在栈中的状态可看出 A 最先进栈,然后 B 进栈,最后 C 进栈。
根据“先进后出”的原则,3 个元素出栈的顺序应该是:C 最先出栈,然后 B 出栈,最后才是 A 出栈。
|
图示
队列
1
2
3
4
| 队列中的元素只能从线性表的一端进,从另一端出,遵循“先入先出”的特点(先进队列的元素也要先出队列)
如上图,队列中有 3 个元素:A、B 和 C,从在队列中的状态可以看出是 A 先进队列,然后 B 进,最后 C 进。
根据“先进先出”的原则,3 个元素出队列的顺序是 A 最先出队列,然后 B 出,最后 C 出。
|
图示

3.2 树存储结构
1
2
3
4
5
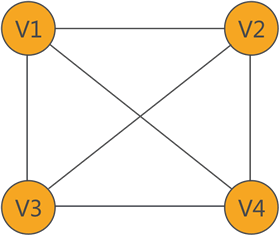
| 树存储结构包含:普通树,二叉树,线索二叉树等。
树存储结构适合存储具有“一对多”关系的数据。
上图中张平只有一个父亲,但他却有两(多)个孩子,这就是“一对多”的关系,满足这种关系的数据可以使用树存储结构。
|
图示
3.3 图存储结构
1
2
3
4
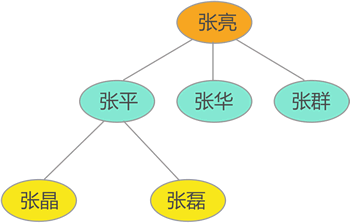
| 图存储结构适合存储具有“多对多”关系的数据
上图从 V1 可以到达 V2、V3、V4,同样,从 V2、V3、V4 也可以到达 V1,
这就是“多对多”的关系,满足这种关系的数据可以使用图存储结构。
|
图示
四 数据的逻辑结构、存储结构(物理结构)
数据存储结构的选择取决于两方面:数据的逻辑结构和存储结构(物理结构)
4.1 逻辑结构
1-逻辑关系
1
2
3
4
5
6
7
8
9
10
| 数据的逻辑结构指数据之间的逻辑关系
从上图的家庭成员关系图中可以看到,张平、张华和张群是兄弟,
他们的父亲是张亮,其中张平有两个儿子,分别是张晶和张磊。
父子、兄弟等这些关系即数据间的逻辑关系,假设要存储这样一张家庭成员关系图,
不仅要存储张平、张华等数据,还要存储它们之间的关系,两者缺一不可。
一组数据成功存储到计算机的衡量标准是要能将其完整的复原。
例如上图所示的成员关系图,如果所存储的数据能将此成员关系图彻底复原,则说明数据存储成功。
|
图示
| 树 |
图 |
 |
 |
2-数据之间的逻辑关系分为三类
1
2
3
4
5
6
7
8
9
| 一对一:
类似集合{1,2,3,...,n}这类的数据,每个数据的左侧有且仅有一个数据与其相邻(除 1 外);
每个数据的右侧也只有一个数据与其相邻(除 n 外),所有的数据都是如此。
一对多:张平有且仅有一个父亲(张亮),但有 2(多)个孩子。
多对多:
从 V1 可以到达 V2、V3、V4,同样,从 V2、V3、V4 也可以到达 V1,
对于 V1、V2、V3 和 V4 来说,它们之间就是“多对多”的关系。
|
3-3 种存储结构分别存储这 3 类逻辑关系的数据
1
2
3
| 线性表:存储具有“一对一”逻辑关系的数据
树结构:存储具有“一对多”关系的数据
图结构:存储具有“多对多”关系的数据
|
可以通过分析数据之间的逻辑关系来决定使用哪种存储结构
(对于使用顺序存储还是链式存储,还要通过数据的物理结构来决定)
4.2 存储结构(物理结构)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
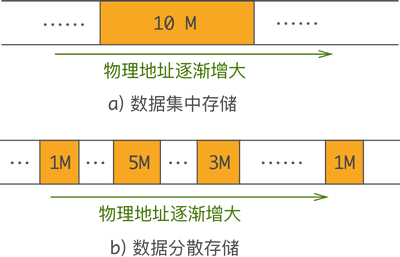
| 数据的存储结构(物理结构)指数据在物理存储空间上选择集中存放还是分散存放。
假设要存储大小为 10G 的数据,则集中存放就如图 3a) 所示,分散存放就如图 3b)所示
如果选择集中存储,就使用顺序存储结构;反之使用链式存储。至于如何选择,主要取决于存储设备的状态以及数据的用途。
集中存储(底层使用数组实现)需要使用一大块连续的物理空间,假设要存储大小为 1G 的数据,
若存储设备上没有整块大小超过 1G 的空间,就无法使用顺序存储,
此时就要选择链式存储,因为链式存储是随机存储数据,占用的都是存储设备中比较小的存储空间。
数据的用途不同,选择的存储结构也不同。
将数据进行集中存储有利于后期对数据进行遍历操作,而分散存储更有利于后期增加或删除数据。
如果后期需要对数据进行大量的检索(遍历),就选择集中存储;
若后期需要对数据做进一步更新(增加或删除),则选择分散存储。
|
图示
五 数据结构和算法的关系和区别
5.1 两者关系
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| 数据结构和算法是两个相互独立的学科,如果非说它们有关系,那也只是互利共赢、1 + 1 > 2的关系。
可以从分析问题的角度去理解数据结构和算法之间的关系。通常解决问题都经过以下两个步骤:
-分析问题,从问题中提取出有价值的数据,将其存储
-对存储的数据进行处理,最终得出问题的答案
数据结构负责解决第一个问题,即数据的存储问题。
针对数据不同的逻辑结构和物理结构,可以选出最优的数据存储结构来存储数据。
而第二个问题属于算法的职责范围。算法即解决问题的方法。
评价一个算法的好坏,取决于在解决相同问题的前提下,哪种算法的效率最高,
而这里的效率指的就是处理数据、分析数据的能力。
因此:数据结构用于解决数据存储问题,
而算法是思考如何利用存储的数据快速无误地解决问题,它们是完全不同的两类学科。
在解决问题的过程中,数据结构要配合算法选择最优的存储结构来存储数据,
而算法也要结合数据存储的特点,用最优的策略来分析并处理数据,由此可以最高效地解决问题。
|
5.2 示例
1
2
3
4
5
6
7
8
| 例如,计算1 + 2 + 3 + 4 + 5的值,可以这样分析:
-计算 1、2、3、4 和 5 的和,首先要选择一种数据存储方式将它们存储起来,
数据之间具有“一对一”的逻辑关系,最适合用线性表来存储。
结合算法的实现,选择顺序表来存储数据(而不是链表),因为顺序表遍历数据比链表更高效。
-接下来选择算法。由于数据集中存放,因此可以设计这样一个算法,
使用一个初始值为 0 的变量 num 依次同存储的数据做“加”运算,最后得到的新 num 值就是最终结果。
|
图示

六 参考










