一 概述
1
2
3
| 1.存储地址是否相同
2.最后一个节点必定相同
3.等长度的一个子链表
|
二 什么是两个单链表是否相交
2.1 概念
1
2
3
4
5
6
7
| 2 个单链表相交意味着它们有公共的节点,公共节点的数量可以是 1 个或多个。
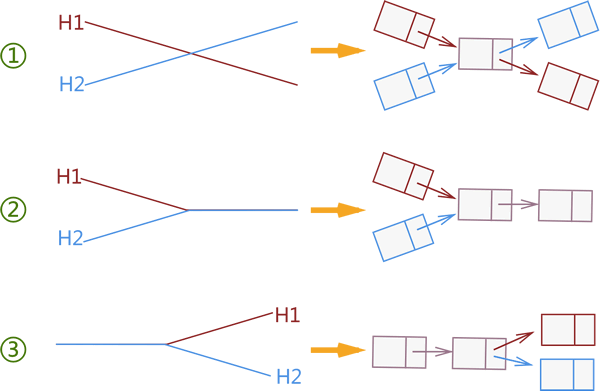
单链表是线性表的一种,如果将 2 个单链表看做 2 条线段的话,下图模拟了 2 条线段相交的所有可能情况
注意:
结合“单链表中每个节点有且仅有 1 个指针域”的特性,上图所示的 3 种情况中只有第 2 种情况符合单链表的特性。
经过以上的分析,本节要验证 2 个单链表是否相交,实际上等同于判断 2 个单链表是否和 ② 的存储结构相同
|
2.2 图示
三 判断 2 个单链表是否相交常用的方法有如下几种
3.1 存储地址是否相同
一、分析
1
2
3
4
5
6
7
8
9
10
| 对于链表 1 中的每个节点,依次和链表 2 中的各节点进行比对,
查看它们的存储地址是否相同,如果相同,则表明它们相交。
注意:此方法中比较的是节点的存储地址,而非数据域中存储的元素。
因为 2 个不相交的链表中很可能存有相同的元素
typedef struct Link {
char elem; // 代表数据域
struct Link * next; // 代表指针域, 指向直接后继元素
}link; // link 为节点名, 每个节点都是一个 link 结构体
|
二、在此基础上,判断 2 个单链表是否相交的实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| // 自定义的 bool 类型
typedef enum bool
{
False = 0,
True = 1
}bool;
// L1 和 L2 为 2 个单链表, 函数返回 True 表示链表相交, 返
// 回 False 表示不相交
bool LinkIntersect(link * L1, link * L2) {
link * p1 = L1;
link * p2 = L2;
// 逐个遍历 L1 链表中的各个节点
while (p1)
{
// 遍历 L2 链表, 针对每个 p1, 依次和 p2 所指节点做比较
while (p2) {
// p1、p2 中记录的就是各个节点的存储地址, 直接比较即可
if (p1 == p2) {
return True;
}
p2 = p2->next;
}
p1 = p1->next;
}
return False;
}
|
三、时间复杂度分析
1
| 通过分析LinkIntersect()函数的实现过程可知,无论2个链表是否相交,此实现方式的时间复杂度为O(n^2)
|
3.2 最后一个节点必定相同
一、优化方案
优化第 1 种实现方案:2 个单链表相交时,这 2 个链表的最后一个节点必定相同。
由此,对以上实现代码进行优化:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| // L1 和 L2 为 2 个单链表, 函数返回 True 表示链表相交, 返
// 回 False 表示不相交
bool LinkIntersect(link * L1, link * L2) {
link * p1 = L1;
link * p2 = L2;
// 找到 L1 链表中的最后一个节点
while (p1->next) {
p1 = p1->next;
}
// 找到 L2 链表中的最后一个节点
while (p2->next)
{
p2 = p2->next;
}
// 判断 L1 和 L2 链表最后一个节点是否相同
if (p1 == p2) {
return True;
}
return False;
}
|
二、时间复杂度:经过优化该函数的时间复杂度缩小为O(n)
3.3 等长度的一个子链表
一、原理图
另一种优化思路:假设 L1 和 L 2 相交,则两个链表中相交部分节点的数量一定是相等的。如下图所示

1
2
3
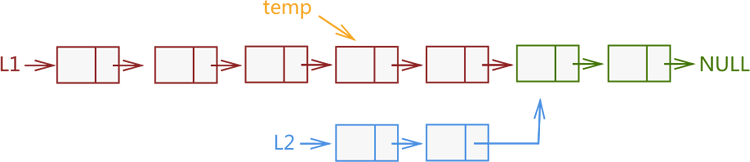
| L1 和 L2 相交,绿色部分节点为 L1 和 L2 链表的相交部分。
从 L1 尾部选取和 L2 链表等长度的一个子链表(即下图中的 temp 子链表),
同时遍历 temp 和 L2 链表,依次判断 2 个遍历节点是否相同,如果相同则表明 L1 和 L2 相交
|
二、代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| // L1 和 L2 为 2 个单链表, 函数返回 True 表示链表相交, 返
// 回 False 表示不相交
bool LinkIntersect(link * L1, link * L2) {
link * plong = L1;
link * pshort = L2;
link * temp = NULL;
int num1 = 0, num2 = 0, step = 0;
// 得到 L1 的长度
while (plong) {
num1++;
plong = plong->next;
}
// 得到 L2 的长度
while (pshort)
{
num2++;
pshort = pshort->next;
}
// 重置 plong 和 pshort, 使 plong 代表较长的链
// 表, pshort 代表较短的链表
plong = L1;
pshort = L2;
step = num1 - num2;
if (num1 < num2) {
plong = L2;
pshort = L1;
step = num2 - num1;
}
// 在 plong 链表中找到和 pshort 等长度的子链表
temp = plong;
while (step) {
temp = temp->next;
step--;
}
// 逐个比较 temp 和 pshort 链表中的节点是否相同
while (temp && pshort) {
if (temp == pshort) {
return True;
}
temp = temp->next;
pshort = pshort->next;
}
return False;
}
|
三、时间复杂度
1
2
3
| 此方法的实现逻辑虽然复杂,但该方法可以找到 2 个单链表相交的交点(相交时的第一个节点),
即LinkIntersect()函数返回 True 时的 temp 指针指向的那个节点。
该方案的时间复杂度也为O(n)
|
四 参考


