一 概述
二 next()数组
2.1 next数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| 在《KMP 快速模式匹配算法》一节中,详细介绍了 KMP 算法解决模式匹配问题的过程(思路、思想)。
文章中提到,计算模式串对应的 NEXT 数组是 KMP 算法的重点和难点,并给出了计算 NEXT 数组的 C 语言实现代码:
void Next(char*T,int *next) {
next[1]=0;
int i=1;
int j=0;
//next[2]=1 可以通过第一次循环直接得出
while (i<strlen(T)) {
if (j==0||T[i-1]==T[j-1]) {
i++;
j++;
next[i]=j;
} else {
j=next[j];
}
}
}
|
2.2 next数组说明
一、
1
2
3
| 假设有一个模式串为 "ABAB",则调用 Next() 函数求得的 NEXT 数组是 {0,1,1,2},如下图所示:
注意观察这个模式串,第一个字符和第三个字符都是 'A',它们对应的 next 值分别是 0 和 1;
同样,第二个字符和第四个字符都是 'B',它们对应的 next 值分别是 1 和 2。
|

二、
1
2
3
4
| 第 3 个字符 'A' 对应的 next 值是 1,意味着当该字符导致模拟匹配失败后,
下次匹配会从模式串的第 1 个字符'A' 开始。
那么问题来了,第一次模式匹配失败说明模式串中的 'A' 和主串对应的字符不相等,
那么下次用第 1 个字符 'A' 与该字符匹配,也绝不可能相等
|
三、
1
2
| 同样的道理,第 4 个字符 'B' 对应的 next 值是 2,意味着当该字符导致模式匹配失败后,
下次模式匹配会从模式串第 2 个字符 'B' 开始,这次匹配也绝不会成功。
|
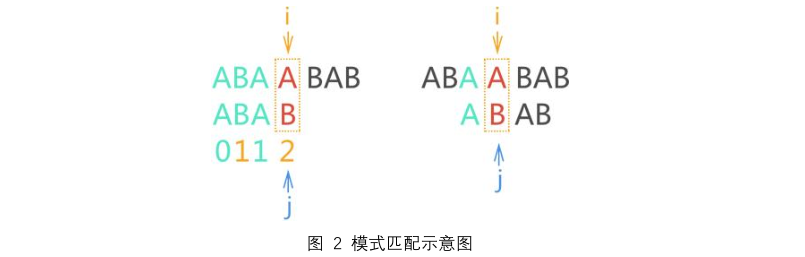
四、举个简单的例子,将模式串 "ABAB" 与主串 "ABAABAB" 进行模式匹配,第一次模式匹配的过程如图所示:
1
2
| 图 2a) 为模式匹配失败时的场景,图 2b) 为第二次模式匹配开始时的场景。
第一次模式匹配失败是因为 'B' 和 'A'不相等,第二次模式匹配还试图匹配 'B' 和 'A',它们绝不可能相等。
|
五
1
2
| 由此可见,KMP 算法的执行效率还有提升的空间。
只要我们优化 NEXT 数组的计算方式,避免出现图 2 这样的无效匹配,KMP 算法的执行效率就能进一步提升。
|
三 优化NEXT数组
我们先以 "ABAB" 模式串为例,思考如何优化它对应的 NEXT 数组。
3.1 优化图示
一、
1
2
3
4
| 实际上 "ABAB" 对应的 NEXT 数组 {0,1,1,2} 中,只需要优化第 3、4 个字符对应的 next 值:
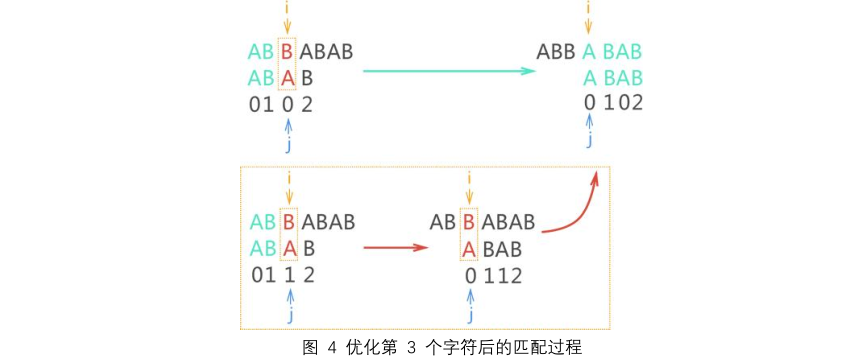
1) 当第 3 个字符 'A' 导致模式匹配失败后,原本它对应的 next 值为 1,但经过前面的分析,下次匹配根本没必
要再拿第一个字符 'A' 与主串比较,直接跳过这次无效的匹配过程即可。实现方法也很简单,就是将第 3 个字符 'A'
的 next 值置为 0,与第 1 个字符的 next 值相等,如下图所示:
|

二、
1
2
| 如上图所示,如果第 3 个字符导致模式匹配失败,根据 KMP 算法的实现思路,执行 j=next[j],j 的值为 0,
则下次匹配开始的位置如下图所示:黄框中的匹配过程(红色箭头标注)是未做优化前的
|
三
1
2
3
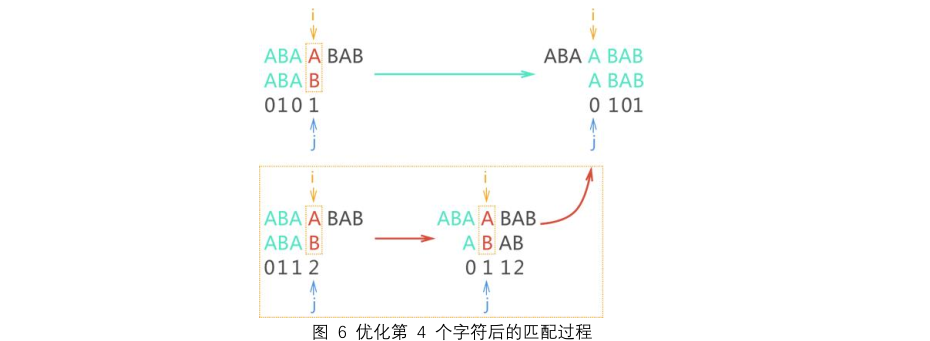
| 2) 当第 4 个字符 'B' 导致模式匹配失败后,原本它对应的 next 值为 2,但经过前面的分析,下次匹配根本没必
要再拿第二个字符 'B' 与主串比较,直接跳过这次无效的匹配过程即可。实现方法也很简单,就是将第 4 个字符 'B'
的 next 值置为 1,与第 2 个字符的 next 值相等,如下图所示:
|

四、
1
2
| 如上图所示,如果第 4 个字符导致模式匹配失败,根据 KMP 算法的实现思路,执行 j=next[j],j 的值为 1,则下
次匹配开始的位置如下图所示:
|
五
1
2
| 显然,经过对 NEXT 数组进行优化,模式匹配的效率得到了提升。
那么,如何修改文章开头的 Next() 函数,使它可以计算出优化后的 NEXT 数组呢?
|
3.2 优化代码
这里给出优化后的 Next() 函数的实现代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| void Next(char*T,int *next) {
next[1]=0;
int i=1;
int j=0;
while (i<strlen(T)) {
if (j==0||T[i-1]==T[j-1]) {
i++;
j++;
if (T[i-1]!=T[j-1]) {
next[i]=j;
} else {
next[i]=next[j];
}
} else {
j=next[j];
}
}
}
|
3.3 说明
一、
1
2
3
4
5
6
7
8
9
10
11
| 注意,对于普通的 Next() 函数,计算得到的 NEXT 数组中前两个值一定是 0 和 1,
但优化后的 Next() 函数求得的 NEXT 数组,第一个值一定为 0,但第二个值不一定为 1。
对比优化前后的 Next() 函数,它们的区别就在于第 10 行代码,这里以计算图 5 "ABAB" 中第 4 个字符 'B' 的
next 值为例,:
1.优化前的 Next() 函数直接执行了 next[i]=j 操作,意味着:当前字符的前缀字符串和后缀字符串相等的个数为
1 个,因此该字符对应的 next 值就为 2。
2.优化后的 Next() 函数,也计算出了当前字符的前缀字符串和后缀字符串的相等个数为 1 个,
但没有立即执行赋值操作,而是将当前字符与第 2 个字符进行了对比:
-如果不相等,直接执行 next[i]=j 操作;
-如果相等,则执行 next[i]=next[j] 操作,即将第 2 个字符对应的 next 值作为第 4 个字符 'B' 对应的next 值。
|
二、匹配效率
1
2
3
4
5
| 经过优化的 Next() 函数,在计算类似 "aaaaaaab" 这种模式串的 NEXT 数组时,可以大幅提升 KMP 算法的匹配效率。例如:
其中 next1 为优化前的 NEXT 数组,next2 为优化后的 NEXT 数组。
假设主串为 "aaaaaaaaaaaaaaaaaaaab",则根据优化后的 NEXT 数组,KMP 算法可以减少大量无效的匹配过程,
少做很多 "无用功",感兴趣的读者可亲自手算两种匹配的过程,效率高低立判。
|

七 参考






