一 概述
1
2
3
4
5
| 1.无序表转化为堆
2.堆排序
3.堆排序解决两个问题
4.堆排序图示
5.示例代码
|
二 无序表转化为堆
2.1 堆
1
2
3
4
5
6
7
8
| 在学习堆排序之前,首先需要了解堆的含义:在含有 n 个元素的序列中,
如果序列中的元素满足下面其中一种关系时,此序列可以称之为堆。
ki ≤ k2i 且 ki ≤ k2i+1
(在 n 个记录的范围内,第 i 个关键字的值小于第 2*i 个关键字,同时也小于第 2*i+1 个关键字)
ki ≥ k2i 且 ki ≥ k2i+1
(在 n 个记录的范围内,第 i 个关键字的值大于第 2*i 个关键字,同时也大于第 2*i+1 个关键字)
|
2.2 无需表转换为堆
1
2
3
4
5
6
| 对于堆的定义也可以使用完全二叉树来解释,
因为在完全二叉树中第 i 个结点的左孩子恰好是第 2i 个结点,右孩子恰好是 2i+1 个结点。
如果该序列可以被称为堆,则使用该序列构建的完全二叉树中,
每个根结点的值都必须不小于(或者不大于)左右孩子结点的值。
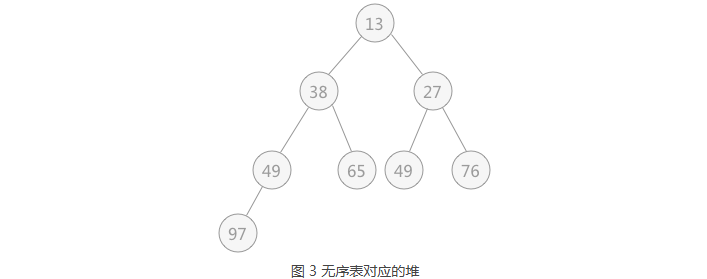
以无序表{49,38,65,97,76,13,27,49}来讲,其对应的堆用完全二叉树来表示为:
|
三 堆排序
1
2
3
4
5
| 提示:堆用完全二叉树表示时,其表示方法不唯一,但是可以确定的是树的根结点要么是无序表中的最小值,要么是最大值。
通过将无序表转化为堆,可以直接找到表中最大值或者最小值,
然后将其提取出来,令剩余的记录再重建一个堆,取出次大值或者次小值,
如此反复执行就可以得到一个有序序列,此过程为堆排序。
|
四 堆排序解决两个问题
1
2
3
| 堆排序过程的代码实现需要解决两个问题:
1.如何将得到的无序序列转化为一个堆?
2.在输出堆顶元素之后(完全二叉树的树根结点),如何调整剩余元素构建一个新的堆?
|
五 堆排序图示
一、步骤1
1
2
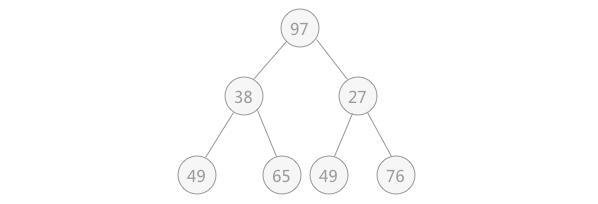
| 首先先解决第 2 个问题。图 3 所示为一个完全二叉树,若去除堆顶元素,
即删除二叉树的树根结点,此时用二叉树中最后一个结点 97 代替,如下图所示:
|
二、步骤2
1
2
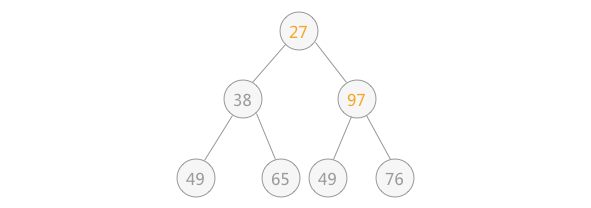
| 此时由于结点 97 比左右孩子结点的值都大,破坏了堆的结构,所以需要进行调整:
首先以 堆顶元素 97 同左右子树比较,同值最小的结点交换位置,即 27 和 97 交换位置:
|
三、步骤3
1
| 由于替代之后破坏了根结点右子树的堆结构,所以需要进行和上述一样的调整,即令 97 同 49 进行交换位置:
|
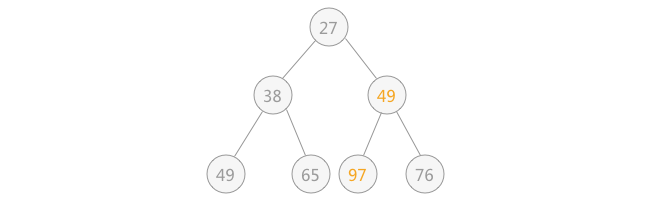
通过上述的调整,之前被破坏的堆结构又重新建立。从根结点到叶子结点的整个调整的过程,被称为“筛选”。
四、步骤4
1
2
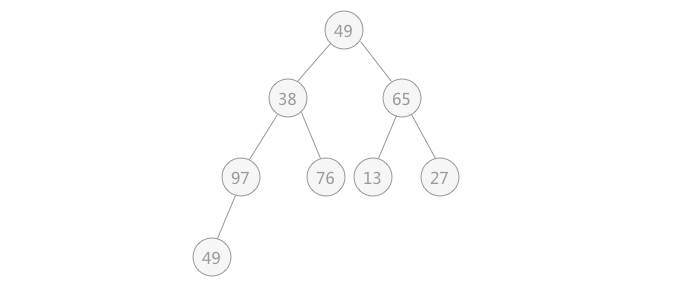
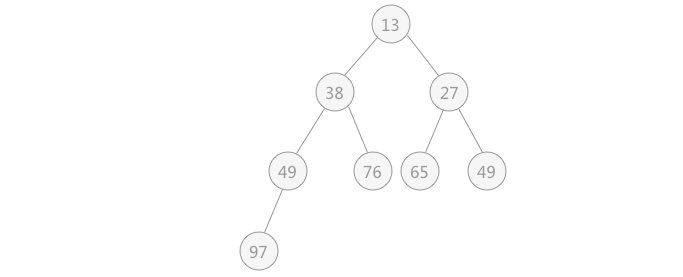
| 解决第一个问题使用的就是不断筛选的过程,如下图所示,
无序表{49,38,65,97,76,13,27,49}初步建立的完全二叉树,如下图所示:
|
五、步骤5
1
2
3
4
5
| 在对上图做筛选工作时,规律是从底层结点开始,一直筛选到根结点。
对于具有 n 个结点的完全二叉树,筛选工作开始的结点为第 ⌊n/2⌋个结点(此结点后序都是叶子结点,无需筛选)。
所以,对于有 9 个结点的完全二叉树,筛选工作从第 4 个结点 97 开始,
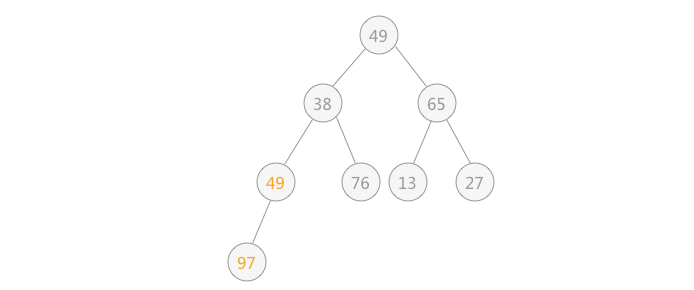
由于 97 > 49 ,所以需要相互交换,交换后如下图所示:
|
六、步骤6
1
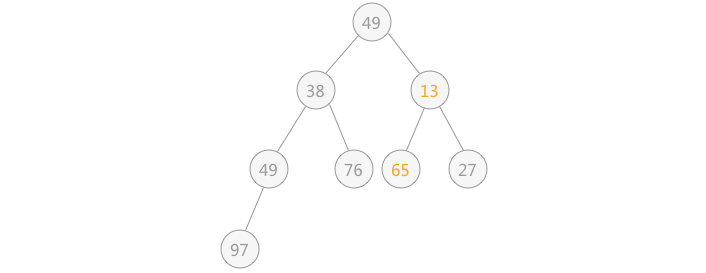
| 然后再筛选第 3 个结点 65 ,由于 65 比左右孩子结点都大,则选择一个最小的同 65 进行交换,交换后的结果为:
|
七、步骤7
1
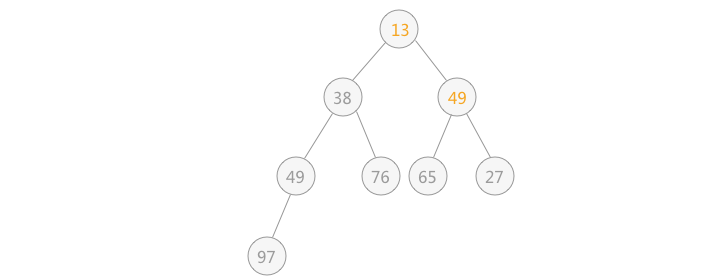
| 然后筛选第 2 个结点,由于其符合要求,所以不用筛选;最后筛选根结点 49 ,同 13 进行交换,交换后的结果为:
|
八、步骤8
1
| 交换后,发现破坏了其右子树堆的结构,所以还需要调整,最终调整后的结果为:
|
六 示例代码
6.1 所以实现堆排序的完整代码为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| #include <stdio.h>
#include <stdlib.h>
#define MAX 9
//单个记录的结构体
typedef struct {
int key;
}SqNote;
//记录表的结构体
typedef struct {
SqNote r[MAX];
int length;
}SqList;
//将以 r[s]为根结点的子树构成堆,堆中每个根结点的值都比其孩子结点的值大
void HeapAdjust(SqList * H,int s,int m){
SqNote rc=H->r[s];//先对操作位置上的结点数据进行保存,放置后序移动元素丢失。
//对于第 s 个结点,筛选一直到叶子结点结束
for (int j=2*s; j<=m; j*=2) {
//找到值最大的孩子结点
if (j+1<m && (H->r[j].key<H->r[j+1].key)) {
j++;
}
//如果当前结点比最大的孩子结点的值还大,则不需要对此结点进行筛选,直接略过
if (!(rc.key<H->r[j].key)) {
break;
}
//如果当前结点的值比孩子结点中最大的值小,则将最大的值移至该结点,由于 rc 记录着该结点的值,所以该结点的值不会丢失
H->r[s]=H->r[j];
s=j;//s相当于指针的作用,指向其孩子结点,继续进行筛选
}
H->r[s]=rc;//最终需将rc的值添加到正确的位置
}
//交换两个记录的位置
void swap(SqNote *a,SqNote *b){
int key=a->key;
a->key=b->key;
b->key=key;
}
void HeapSort(SqList *H){
//构建堆的过程
for (int i=H->length/2; i>0; i--) {
//对于有孩子结点的根结点进行筛选
HeapAdjust(H, i, H->length);
}
//通过不断地筛选出最大值,同时不断地进行筛选剩余元素
for (int i=H->length; i>1; i--) {
//交换过程,即为将选出的最大值进行保存大表的最后,同时用最后位置上的元素进行替换,为下一次筛选做准备
swap(&(H->r[1]), &(H->r[i]));
//进行筛选次最大值的工作
HeapAdjust(H, 1, i-1);
}
}
int main() {
SqList * L=(SqList*)malloc(sizeof(SqList));
L->length=8;
L->r[1].key=49;
L->r[2].key=38;
L->r[3].key=65;
L->r[4].key=97;
L->r[5].key=76;
L->r[6].key=13;
L->r[7].key=27;
L->r[8].key=49;
HeapSort(L);
for (int i=1; i<=L->length; i++) {
printf("%d ",L->r[i].key);
}
return 0;
}
|
6.2 运行结果为
6.3 说明
1
2
| 提示:代码中为了体现构建堆和输出堆顶元素后重建堆的过程,
堆在构建过程中,采用的是堆的第二种关系,即父亲结点的值比孩子结点的值大;重建堆的过程也是如此。
|
6.4 时间复杂度
1
2
3
| 堆排序在最坏的情况下,其时间复杂度仍为 O(nlogn)。
这是相对于快速排序的优点所在。
同时堆排序相对于树形选择排序,其只需要一个用于记录交换(rc)的辅助存储空间,比树形选择排序的运行空间更小。
|
七 参考








