1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
| void RB_Insert_Fixup(RBT_Root* T, RB_TREE* x) {
//首先判断其父结点颜色为红色时才需要调整;为黑色时直接插入即可,不需要调整
while (x->p->color == RED) {
//由于还涉及到其叔叔结点,所以此处需分开讨论,确定父结点是祖父结点的左孩子还是右孩子
if (x->p == x->p->p->left) {
RB_TREE * y = x->p->p->right;//找到其叔叔结点
//如果叔叔结点颜色为红色,此为第 1 种情况,处理方法为:父结点颜色改为黑色;叔叔结点颜色改为黑色;祖父结点颜色改为红色,
将祖父结点赋值为当前结点,继续判断;
if (y->color == RED) {
x->p->color = BLACK;
y->color = BLACK;
x->p->p->color = RED;
x = x->p->p;
} else {
//反之,如果叔叔结点颜色为黑色,此处需分为两种情况:1、当前结点时父结点的右孩子;2、当前结点是父结点的左孩子
if (x == x->p->right) {
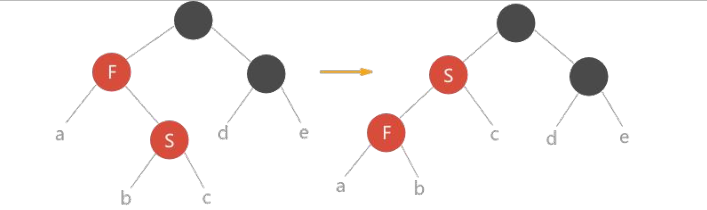
//第 2 种情况:当前结点时父结点的右孩子。解决方案:将父结点作为当前结点做左旋操作。
x = x->p;
rbTree_left_rotate(T, x);
} else {
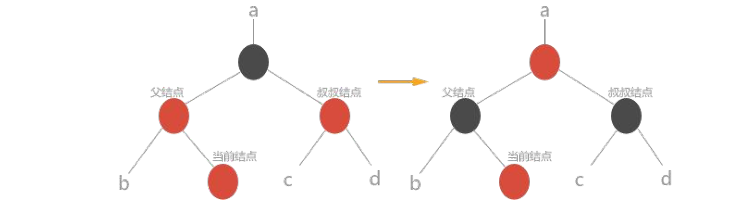
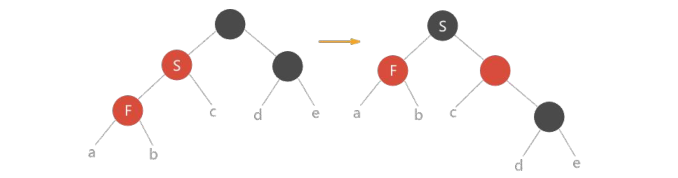
//第 3 种情况:当前结点是父结点的左孩子。解决方案:将父结点颜色改为黑色,祖父结点颜色改为红色,从祖父结点处进行
右旋处理。
x->p->color = BLACK;
x->p->p->color = RED;
rbTree_right_rotate(T, x->p->p);
}
}
} else { //如果父结点时祖父结点的右孩子,换汤不换药,只需将以上代码部分中的 left 改为 right 即可,道理是一样的。
RB_TREE * y = x->p->p->left;
if (y->color == RED) {
x->p->color = BLACK;
y->color = BLACK;
x->p->p->color = RED;
x = x->p->p;
} else {
if (x == x->p->left) {
x = x->p;
rbTree_right_rotate(T, x);
} else {
x->p->color = BLACK;
x->p->p->color = RED;
rbTree_left_rotate(T, x->p->p);
}
}
}
}
T->root->color = BLACK;
}
//插入操作分为 3 步:1、将红黑树当二叉查找树,找到其插入位置;2、初始化插入结点,将新结点的颜色设为红色;3、通过调用调整函数,将二叉
查找树重新改为红黑树
void rbTree_insert(RBT_Root**T, int k) {
//1、找到其要插入的位置。解决思路为:从树的根结点开始,通过不断的同新结点的值进行比较,最终找到插入位置
RB_TREE * x, *p;
x = (*T)->root;
p = x;
while(x != (*T)->nil) {
p = x;
if(k<x->key) {
x = x->left;
} else if(k>x->key) {
x = x->right;
} else {
printf("\n%d 已存在\n",k);
return;
}
}
//初始化结点,将新结点的颜色设为红色
x = (RB_TREE *)malloc(sizeof(RB_TREE));
x->key = k;
x->color = RED;
x->left = x->right =(*T)->nil;
x->p = p;
//对新插入的结点,建立与其父结点之间的联系
if((*T)->root == (*T)->nil) {
(*T)->root = x;
} else if(k < p->key) {
p->left = x;
} else {
p->right = x;
}
//3、对二叉查找树进行调整
RB_Insert_Fixup((*T),x);
}
|